-
ВЫ СТУДЕНТ МИЭП (Международный Институт Экономики и Права)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Теория вероятности и математическая статистика МИЭП
О НАС
Меня зовут Сергей, 10 лет я решаю тесты и пишу работы по данному предмету, для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Высокий процент сдачи тестов.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2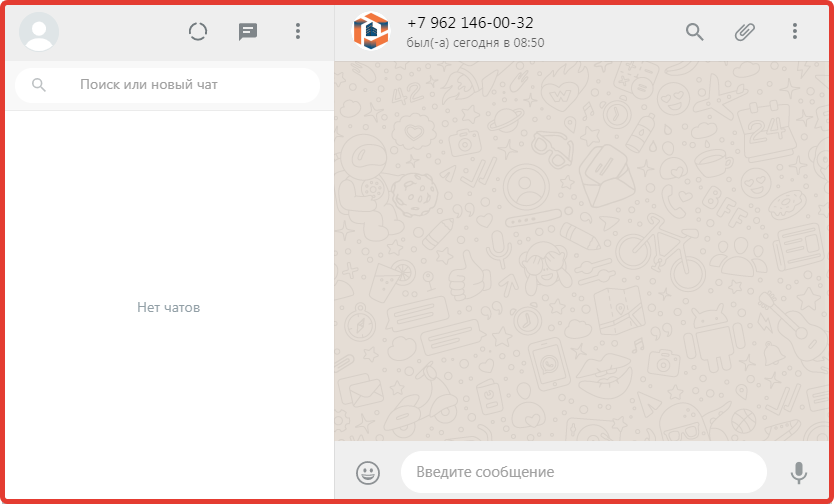
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3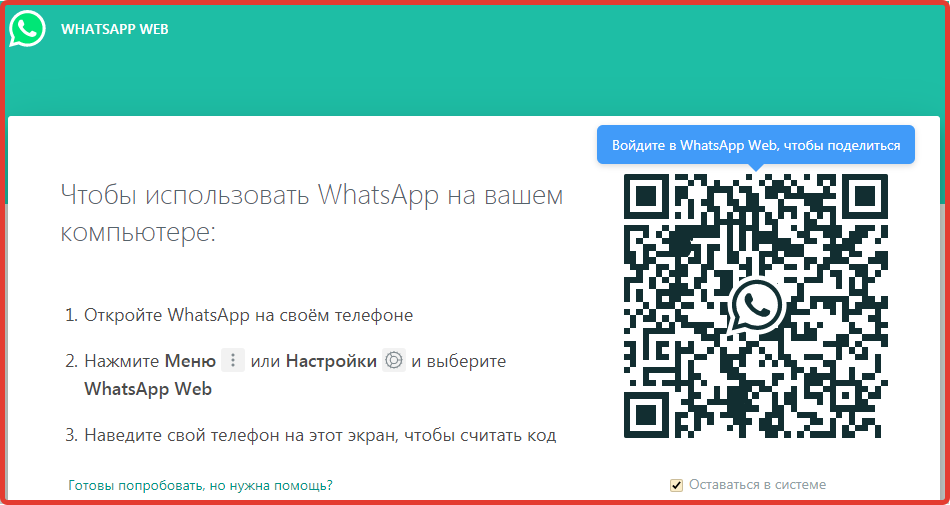
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:
Курсовая работа
По данному предмету, данный вид работы не предусмотрен.
Мы, ни раз, писали КР (курсовые работы) по данному предмету и уверенно можем сказать: "Сделаем по всем требованиям". Вам останется только сдать работу, пишем работу полностью, оформляем, вставляем титульный лист, все работы проверям на антиплагиат, если будут замечания исправляем бесплатно.
Если необходима помощь, доверьте написания КР нам, так как, мы знакомы с требованиями Вашего ВУЗа, работаем профессионально и оперативно.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Ответы на тесты МИЭП
Тестирование проходит на официальном сайте МИЭП http://sdo1.miep.ru и http://sdo.miep.ru Оценка выставляется, по первому положительному результату.
Вопросы для подготовки к тестированию:
-
Пусть событие А={1,2,3},а событие В={1,2,3,4,5,6}. Укажите верное высказывание.
Пусть событие А={1,2,3},а событие В={1,2,3,4,5,6}. Укажите верное высказывание. (По заданию ППЗ № 3 Тема № 1)
Дисперсия случайной величины Х равна 5. Чему равно значение дисперсии D(-2X) (По заданию ППЗ № 1
Тема № 5)
Ввод ответа вручную с клавиатуры
При обследовании отдельного региона фирмой, предоставляющей интернет-услуг, выявлено, что (в среднем) из каждых 100 семей, 80 имеют компьютер, подключенный к интернет. Оценить вероятность того, что из 400 семей данного микрорайона, от 300 до 360 семей имеют компьютер, поключенный к интернет.
Рассматриваются две случайные величины X и Y. Их математическое ожидание и дисперсия соответственно равны: М(X)=3; D(X)=2; M(Y)=2; D(Y)=1. Укажите верные соотношения.Рассматриваются две случайные величины X и Y. Их математическое ожидание и дисперсия соответственно равны:М(X)=3; D(X)=2; M(Y)=2; D(Y)=1. Укажите верные соотношения.
Рассматриваются две случайные величины X и Y. Их математическое ожидание и дисперсия соответственно равны: М(X)=3; D(X)=2; M(Y)=2; D(Y)=1. Укажите верные соотношения.
Рассматриваются две случайные величины X и Y. Их математическое ожидание и дисперсия соответственно равны: М(X)=3; D(X)=2; M(Y)=2; D(Y)=1. Укажите верные соотношения. (По заданию ППЗ № 1 Тема № 5)
Какая из следующих формул используется для вычисления числа размещения? (По заданию ППЗ № 1
Тема № 2)
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P.
Укажите по какой формуле вычисляется дисперсия D(X).
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P. Укажите по какой формуле вычисляется математическое ожидание M(X)
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P. Укажите по какой формуле вычисляется дисперсия D(X).
Брошены две игральные кости. Какая из следующих совокупностей полученного числа образует полную группу событий?
Брошены две игральные кости. Какая из следующих совокупностей очков образует полную группу событий? (По заданию ППЗ № 4
Тема № 1)
Монета бросается 2 раза, какова вероятность P выпадения подряд двух гербов?
Монета бросается 2 раза,какова вероятность P выпадения подряд двух гербов? (По заданию ППЗ № 1
Тема № 3)
На рисунке представлены графики нормальных распределений N1, N2, N3.Расположите эти распределения в порядке возрастания их математического ожидания.
На рисунке представлены графики нормальных распределений N1, N2, N3.Расположите эти распределения в порядке возрастания их дисперсии. (По
На рисунке представлены графики нормальных распределений N1, N2, N3.Расположите эти распределения в порядке возрастания их дисперсии. (По заданию ППЗ № 4
Тема № 7)
Чему равно математическое ожидание M(X-Y) разности двух случайных величин X и Y,а если известны значения математических ожиданий каждой из них:M(X)=3; M(Y)=4? (По заданию ППЗ № 1
Тема № 5)
Чему равно математическое ожидание M(X+Y) суммы двух случайных величин X и Y,а если известны значения математических ожиданий каждой из них:M(X)=3; M(Y)=4?
Найти математическое ожидание дискретной случайной величины Х, заданной следующим законом распределенияУкажите названия вероятностей, входящих в формулу Байеса. (По заданию ППЗ № 9 Тема № 3)
Пусть событие А={1,2.3.4,5}, а событие В={5,4,3,2,1}. Укажите верное высказывание. (По заданию ППЗ № 3
Тема № 1)
Чему равна дисперсия разности D(X-Y) двух независимых случайных величин X и Y, если известны значения дисперсий каждой из них: D(X)=3 и D(Y)=4?
Что значат записанные ниже формулы.
где совокупность гипотез Hi, i=L,…,n образует полную группуЧто означают записанные ниже формулы. (По заданию ППЗ № 11 Тема № 3)
Различаются ли понятия "перестановки из трех элементов" и "размещения из трех элементов по три"?
Чему равна дисперсия суммы D(X+Y) двух независимых случайных величин X и Y, если известны значения дисперсий каждой из них: D(X)=3 и D(Y)=4? (По заданию ППЗ № 1 Тема № 5)
Дисперсия случайной величины Х равна 5. Чему равно значение дисперсии D(3X+6)
Дисперсия случайной величины Х равна 5. Чему равно значение дисперсии D(3X+6) (По заданию ППЗ № 1 Тема № 5)
Математическое ожидание случайной величины Х равна 5:M(X)=5. Чему равно значение математического ожидания М(Х-1)?
Математическое ожидание случайной величины Х равна 5:M(X)=5. Чему равно значение математического ожидания М(Х-1)? (По заданию ППЗ № 1
Тема № 5)
Математическое ожидание случайной величины Х равна 5:M(X)=5.
Чему равно значение математического ожидания М(-2Х)?
В серии из n независимых испытаний, проводимых по схеме Бернулли, наблюдается наступление события А. Что означают указанные ниже компоненты формулы Бернулли? Pm,n=Cmnpmqn-m, где q=1-p. Что означают в этой формуле:
1) Pm,n 2) Cmn 3) pВ серии из n независимых испытаний, проводимых по схеме Бернулли, наблюдается наступление события А. Что означают указанные ниже компоненты формулы Бернулли? (По заданию ППЗ № 12
Тема № 3)Начало формы- Установить последовательность ответов
Пусть А –случайное событие, вероятность которого отлична от нуля и 1; Ω –достоверное и Ø – невозможное событие. События B, C, и D определены как: B=A+A; C=A+ Ω; D=A* Ø
Чему равно значение среднего квадратического отклонения числа 4? (По заданию ППЗ № 5 Тема № 5)
Чему равно значение среднего квадратического отклонения числа 4?
Чему равно значение среднего квадратического отклонения числа 4? (По заданию ППЗ № 5
Тема № 5)
Дисперсия случайной величины X равна 5: D(X)=5. Чему равно значение дисперсии D(-2X)?
Математическое ожидание и дисперсия случайной величины X, соответственно,равны М(Х)=3;D(X)=2. Расположите следующие выражения в порядке возрастания их значений.
Математическое ожидание и дисперсия случайной величины X, соответственно, равны М(Х)=3;D(X)=2. Расположите следующие выражения в порядке возрастания их значений. (По заданию ППЗ № 2
Тема № 5)
Математическое ожидание случайной величины Х равна 5:M(X)=5. Чему равно значение математического ожидания М(3Х+6)? (По заданию ППЗ № 1 Тема № 5)
Дисперсия случайной величины Х равна 5.
Чему равно значение дисперсии D(X-1)
Понятие факториала. Какое из следующих выражений неверно?
Понятие факториала. Какое из следующих выражений неверно? (По заданию ППЗ № 1 Тема № 2)
Какое из следующих выражений неверно?
Сравните два числа и укажите правильный ответ. Сравните два числа. Какое из них больше? Какое из чисел больше 10! или 1010?
Сравните два числа и укажите правильный ответ. (По заданию ППЗ № 1
Тема № 2)
Охарактеризуйте событие: 2х2=5
Чему равна сумма противоположных событий?
Чему равна сумма противоположных событий? (По заданию ППЗ № 2
Тема № 1)
Чему равно произведение противоположных событий ?
Чему равно произведение противоположных событий? (По заданию ППЗ № 3
Тема № 1)
Брошены две игральные кости. Какая из следующих совокупностей полученного числа очков образует полную группу событий?
События образуют полную группу если они:
События образуют полную группу если они: (По заданию ППЗ № 1
Тема № 1)
Чему равна сумма случайных событий, образующих полную группу?
Чему равна сумма случайных событий, образующих полную группу? (По заданию ППЗ № 5
Тема № 1)
Пусть событие А=1, 2, 3, а событие B=1, 2, 3, 4, 5, 6. Укажите верное высказывание.
Пусть событие А=1,2,3,4,5, а событие B=5,4,3,2,1. Укажите верное высказывание.
Сколько элементов содержит множество элементарных событий, описывающих результат бросания игрального кубика?
Сколько элементов содержит множество элементарных событий, описывающих результат бросания игрального кубика? (По заданию ППЗ № 3 Тема № 1)
Какая из следующих формул используется для вычисления числа размещений?
Размещения и перестановки (По заданию ППЗ № 2
Тема № 2)
Размещения и перестановки. Пусть Pn – число возможных перестановок из n элементов, и Аmn- число размещений из n элементов по m (n>m). Каково соотношение между величинами Pn и Аmn? Укажите верный ответ:
Различаются ли понятия 'перестановки из трех элементов' и 'размещения из трех элементов по три' ?
Свойства сочетаний. Пусть Cmn – число сочетаний из n элементов по m
Свойства сочетания (По заданию ППЗ № 4
Тема № 2)
Монета бросается два раза. Какова вероятность P выпадения подряд двух гербов?
Монета бросается три раза. Какова вероятность Р выпадения подряд трех гербов? (По заданию ППЗ № 2
Тема № 3)
Монета бросается три раза. Какова вероятность P выпадения подряд трех гербов?
Пусть А и В - случайные события. Сравните величины P(A+B) и Р(А)+Р(В) и укажите правильный ответ.
Пусть А и В-случайные события. Сравните величины Р(А+В) и Р(А)+Р(В) и укажите правильный ответ.
Пусть А и В-случайные события. Сравните величины Р(А+В) и Р(А)+Р(В) и укажите правильный ответ.
Чему равна вероятность суммы противоположных событий? (По заданию ППЗ № 3
Тема № 3)
Чему равна вероятность произведения противоположных событий? (По заданию ППЗ № 3
Тема № 3)
Пусть А - случайное событие, вероятность которого - Р(А)=0,3. Чему равна вероятность события Р(А+А)?
Пусть А - случайное событие, вероятность которого - Р(А)=0,3. Чему равна вероятность события Р(А+А) ?
Пусть А - случайное событие, вероятность которого - Р(А)=0,3. Чему равна вероятность произведения событий Р(А*А)?
Вероятность произведения достоверного и случайного событий. Пусть Ω – достоверное событие и А случайное событие, вероятность которого – P(A)=0,3. Чему равна вероятность произведения этих событий - P(А∙Ω)? Укажите верный ответ среди перечисленных.
Вероятность произведения достоверного и случайного событий. (По заданию ППЗ № 6 Тема № 3)
Вероятность суммы невозможного и случайного событий. Пусть Ø – невозможное событие и А - случайное событие, вероятность которого – P(A)=0,3. Чему равна вероятность суммы этих событий - P(А+Ø)? Укажите верный ответ среди перечисленных.
Вероятность суммы невозможного и случайного событий (По заданию ППЗ № 8 Тема № 3)
Вероятность произведения невозможного и случайного событий. Пусть Ø – невозможное событие и А - случайное событие, вероятность которого – P(A)=0,3. Чему равна вероятность произведения этих событий - P(А∙Ø)? Укажите верный ответ среди перечисленных.
Вероятность произведения невозможного и случайного событий (По заданию ППЗ № 7
Тема № 3)
Чему равна вероятность Р суммы событий, образующих полную группу?
Чему равна вероятность Р суммы событий, образующих полную группу?
Чему равна вероятность Р суммы событий, образующих полную группу? 26
(По заданию ППЗ № 1
Тема № 3)
Вероятность суммы достоверного и случайного события. Пусть Ω – достоверное событие и А случайное событие, вероятность которого – P(A)=0,3. Чему равна вероятность произведения этих событий - P(А+Ω)? Укажите верный ответ среди перечисленных.
Вероятность суммы достоверного и случайного события. (По заданию ППЗ № 1
Тема № 3)
Априорная вероятность. (По заданию ППЗ № 9
Тема № 3)
Ниже записана формула Байеса:
где совокупность гипотез Hi, i=L,…,n образует полную группу. Как в этой формуле обозначена априорная вероятность?
Априорная вероятность. Ниже записана формула Байеса:
где совокупность гипотез Hi, i=L,…,n образует полную группу. Как в этой формуле обозначена априорная вероятность?
Априорная вероятность.
Апостериорная вероятность. Ниже записана формула Байеса:
где совокупность гипотез Hi, i=L,…,n образует полную группу. Как в этой формуле обозначена апостериорная вероятность?
Апостериорная вероятность. (По заданию ППЗ № 10 Тема № 3)
Формула полной вероятности. (По заданию ППЗ № 11
Тема № 3)
где совокупность гипотез Hi, i=L,…,n образует полную группу
Формула полной вероятности. Укажите формулу вычисления полной вероятности события:
где совокупность гипотез Hi, i=L,…,n образует полную группу
Можно ли считать схемой Бернулли многократное подбрасывание монеты (испытания по типу 'орел-решка')?
Можно ли считать схемой Бернулли многократное подбрасывание монеты (испытание по типу "орел-решка")?
Можно ли считать схемой Бернулли многократное подбрасывание монеты (испытание по типу "орел-решка")? (По заданию ППЗ № 4 Тема № 4)
Формула Бернулли. Формула Бернулли имеет вид: Pm,n=Cmnpmqn-m, где q=1-p
Что означает в этой формуле Pm,n?
Формула Бернулли. (По заданию ППЗ № 2 Тема № 4)
Каковы причины использования асимптотических приближений формулы Бернулли ?
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P. Укажите, по какой формуле вычисляется дисперсия D(X):
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P. Укажите по какой формуле вычисляется математическое ожидание M(X) (По заданию ППЗ № 2
Тема № 5)
Формула Пуассона имеет вид: (По заданию ППЗ № 10
Тема № 5)
Что означает в этой формуле Pm,n?
Формула Пуассона (По заданию ППЗ № 10
Тема № 5)
Укажите критерии использования формулы Пуассона. Формула Пуассона имеет вид:
Укажите критерии использования формулы Пуассона. (По заданию ППЗ № 9 Тема № 5)
Законом редких явлений называют:
Законом редких явлений называют: (По заданию ППЗ № 3
Тема № 5)
Локальная формула Муавра-Лапласа. (По заданию ППЗ № 4 Тема № 5)
Что означает в этой формуле Pm,n?
Укажите критерий использования локальной теоремы (формулы) Муавра-Лапласа (см. ниже). Локальная формула Муавра-Лапласа имеет вид:
Укажите критерий использования локальной теоремы (формулы) Муавра-Лапласа (см. ниже) (По заданию ППЗ № 5 Тема № 5)
Начало формыУкажите критерий использования локальной теоремы(формулы) Муавра-Лапласа.
Конец формыУкажите свойство функции Гаусса. (см. ниже):
Укажите свойство функции Гаусса. (По заданию ППЗ № 1 Тема № 6)
Интегральная формула Муавра-Лапласа (По заданию ППЗ № 10 Тема № 5)
Что означает в этой формуле Pn(a≤m≤b)?
Укажите критерий использования интегральной теоремы (формулы) Муавра-Лапласа. Интегральная формула Муавра-Лапласа имеет вид:
Свойства функции Лапласа (По заданию ППЗ № 1
Тема № 6)
Какая характеристика случайной величины имеет смысл ее среднего значения? (По заданию ППЗ № 3
Тема № 6)
Чему равно математическое ожидание M(X+Y) суммы двух случайных величин X и Y, если известны значения математических ожиданий каждой из них: M(X) = 3 и M(Y) = 4 ?
Чему равно математическое ожидание M(X-Y) разности двух случайных величин X и Y, если известны значения математических ожиданий каждой из них: M(X) = 3 и M(Y) = 4 ?
Математическое ожидание случайной величины X равна 5: М(X) = 5. Чему равно значение математического ожидания М(X-1) ?
1Математическое ожидание случайной величины X равна 5: М(X) = 5. Чему равно значение математического ожидания М(-2X) ?
Математическое ожидание случайной величины X равна 5: М(X) = 5. Чему равно значение математического ожидания М(3X+6) ?
Чему равно значение математического ожидания числа 5: M(5) = ?
Чему равно значение математического ожидания числа 5?
Чему равно значение математического ожидания числа 5? (По заданию ППЗ № 1
Тема № 5)
Найти математическое ожидание дискретной случайной величины X, заданной следующим законом распределения:Какая характеристика случайной величины определяет степень ее рассеяния? (По заданию ППЗ № 4
Тема № 6)
Чему равна дисперсия суммы D(X+Y) двух независимых случайных величин X и Y, если известны значения дисперсий каждой из них: D(X)=3 и D(Y)=4?
Чему равна дисперсия разности D(X-Y) двух независимых случайных величин X и Y, если известны значения дисперсий каждой из них: D(X)=3 и D(Y)=4?
Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии D(X-1) ?
Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии D(-2X) ?
Дисперсия случайной величины X равна 5: D(X) = 5. Чему равно значение дисперсии D(3X+6) ?
Чему равно значение дисперсии числа 5?
Чему равно значение дисперсии числа 5: D(5) = ?
Среднее квадратическое отклонение равно:
Охарактеризуйте множество значений дискретной случайной величины (укажите наиболее полный ответ):
Задача: Случайная величина X принимает три возможных значения x1=2; x2=5; x3=8. Известны вероятности первых двух возможных значений: p1=0,4 и p2=0,15. Найти вероятность значения x3; p3=?Множество значений непрерывной случайной величины является:
Какое значение непрерывной случайной величины Х определяет ее медиана Ме(Х) ?
Мода Mo(X) случайной величины Х характеризует (укажите верный ответ):
Функция распределения. Вероятность какого события определяет функция распределения F(X) cлучайной величины X?
Наименьшее значение функции распределения. Непрерывная случайная величина X определена на всей числовой оси. Чему равно предельное значение ее функции распределения F(x) при x->-∞ (укажите верный ответ среди ниже перечисленных)?
Наибольшее значение функции распределения. Непрерывная случайная величина X определена на всей числовой оси. Чему равно предельное значение ее функции распределения F(x) при x->-∞ (укажите верный ответ среди ниже перечисленных)?
Каким из перечисленных ниже свойств обладает функция распределения случайной величины?
Какие значения может принимать биномиально распределенная случайная величина Х ? P(X=m)=Cmnpmqn-m, где: 0<p<1, q=1-p
Чему равно математическое ожидание M(X) случайной величины Х, распределенной по биномиальному закону: P(X=m)=Cmnpmqn-m, где: 0<p<1, q=1-p
Чему равна дисперсия D(X) случайной величины Х, распределенной по биномиальному закону: P(X=m)=Cmnpmqn-m, где: 0<p<1, q=1-p
Какие значения может принимать случайная величина Х, описываемая законом распределения Пуассона ?
Распределение Пуассона. Математическое ожидание. Чему равно математическое ожидание M(X) случайной величины X распределенной по закону Пуассона:
Распределение Пуассона. Дисперсия. Чему равно D(X) случайной величины X распределенной по закону Пуассона:
Математическое ожидание случайной величины X, имеющей Пуассоновский закон распределения, равно 4: M(X) = 4. Чему равна дисперсия D(X) этой случайной величины?
Геометрическое распределение дискретной случайной величины. Согласно распределению: случайная дискретная величина X, имеет геометрическое распределение с параметром p, принимает бесконечное (но счетное) множество значений 1,2, … , m, … с вероятностями: P(X=m)=pqm-1, где 0<p<1, q=1-p.
Укажите какова смысловая интерпретация такой случайной величины Х:
Равномерное распределение. Охарактеризуйте плотность вероятности случайной величины, равномерно распределенной на отрезке [a, b]:
Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в произвольный момент времени. Какова вероятность - P того, что ждать пассажиру придется не больше полминуты?
Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в произвольный момент времени. Определить математическое ожидание M(X) случайной величины X - времени ожидания поезда.
Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [2,6]. Чему равно ее математическое ожидание M(X) ?
Смысловое значение параметра 'a' нормального закона распределения случайной величины (см. ниже) это:
Смысловое значение параметра 'сигма квадрат' нормального распределения (закона Гаусса).
Влияние математического ожидания (параметра 'a') на график плотности вероятности нормального закона (закона Гаусса) распределения случайной величины (см. ниже) характеризуется:
Сравнение математических ожиданий. M(X1) и М(Х2) нормально распределенных случайных величин Х1 и Х2 (см. рисунок ниже).
Укажите верный ответ:
Уменьшение дисперсии (параметра 'сигма квадрат') нормального закона (закона Гаусса) распределения случайной величины (см. ниже) приводит к следующему изменению графика кривой распределения:
Сравнение дисперсий D(X1) и D(X2) нормально распределенных случайных величин X1 и X2 (см. рисунок ниже).
Укажите верный ответ:
Стандартным (нормированным) законом распределения N(0;1) называется:
Правило трех сигм.
Значение закона больших чисел.
Значение несобственного интеграла от плотности вероятности. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен:
К чему стремится частость наблюдаемого события при неограниченном увеличении числа испытаний в схеме Бернулли ?
Из генеральной совокупности отобраны десять элементов по принципу: брался каждый восьмой по порядку элемент генеральной совокупности. Как называется такой способ отбора?
Как называется варианта, характеризующая наибольшую частоту в выборке?
Уровень значимости при проверке статистической гипотезы задан в 10%. Какова возможность ошибки первого рода?
Какая из следующих числовых характеристик выборки является смещенной оценкой?
Найти моду для генеральной совокупности заданной вариационным рядом:Найти генеральную среднюю генеральной совокупности, заданной следующим вариационным рядом:
Найти медиану для генеральной совокупности заданной вариационным рядом:
Определить выборочную среднюю для следующей выборки:
Найти выборочную среднюю следующей выборки из генеральной совокупности:
К каким соединениям относится свойство симметрии?
Укажите, какое из перечисленных ниже свойств числовых характеристик случайной величины записано неправильно (предполагая, что X и Y - независимые случайные величины) ?
Начало формыУстановите соответствие между числом сочетаний, перестановок и формулами для их вычисления
Конец формыРазмах варьирования вариационного ряда –1, 0, 2, 3, 4, 5, 7, 8, 10, 12, 14 равен
Размах варьирования вариационного ряда:
–2, 0, 2, 3, 4, 5, 7, 8, 10, 12, 15 равен …
Впишите недостающие слова в название закона распределения случайной величины
Начало формыКонец формы
Впишите недостающие слова в название закона распределения случайной величины
(со строчной буквы):
1. Непрерывная случайная величина имеет закон распределения на отрезке [а,b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его;
2. Непрерывная случайная величина имеет закон распределения (закон Гаусса) с параметрами а и b2, если ее ппотность вероятности имеет вид:
3. Дискретная случайная величина имеет закон распределена с параметрам! n и р , если она принимает значения
0,1, 2, ...,m вероятностями: Р[Х. = т •= С* pMq™ , где 0<р<1, cpl- р.Установить последовательность ответов (По заданию ППЗ № 4
Тема № 3)
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
Точечная оценка математического ожидания нормально распределенного количественного признака равна 6,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
(Основная гипотеза имеет вид H0 : p=0,6. Тогда конкурирующей может являться гипотеза …
Основная гипотеза имеет вид H0 : p=0,4. Тогда конкурирующей может являться гипотеза …
Выборочное уравнение прямой линии регрессии
Выборочное уравнение прямой линии регрессии Y на X имеет вид y = – 6,0 – 1,5x.
Тогда выборочный коэффициент регрессии равен …
Выборочное уравнение прямой линии регрессии Y на X имеет вид y = – 6,0 – 1,5x. Тогда выборочный коэффициент регрессии равен …
Соотношением вида Р(К < -2,09) = 0,025 можно определить …
Двусторонняя критическая область может определяться из соотношения …
Сопоставьте имена ученых с их вкладом в развитие Теории вероятностей:Статистическое распределение выборки имеет вид
Статистическое распределение выборки имеет вид
Варианты ответов
Правосторонняя критическая область может определяться из соотношения …
Дан доверительный интервал (16,64; 18,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …Дан доверительный интервал (16, 64; 18,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …
Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами …
Дан доверительный интервал (32,06; 41,18) для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
Дан доверительный интервал (32,06; 41,18) для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
Из генеральной совокупности извлечена выборка объема n=114, полигон частот которой имеет вид:
Из генеральной совокупности извлечена выборка объема n=120, полигон частот которой имеет вид:
Из генеральной совокупности извлечена выборка объема
Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочный коэффициент корреляции может быть равен …
Варианты ответов
Начало формыСтатистическое распределение выборки имеет вид (По заданию ППЗ № 2 Тема № 8)
Конец формыСтатистическое распределение выборки имеет вид: (По заданию ППЗ № 2 Тема № 8)
Статистическое распределение выборки имеет вид
Тогда значение относительной частоты равно …
Мода вариационного ряда 2, 4, 5, 7, 7, 7, 9, 9, 11, 12 равна …
Мода вариационного ряда 2, 4, 5, 7, 7, 7, 9, 9, 11, 12 равна …
Выборочное уравнение прямой линии регрессии X на Y имеет вид: x = – 4,72 + 2,36y. Тогда выборочный коэффициент корреляции может быть равен …
Дан доверительный интервал (12,02; 16,28) для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
Для независимых случайных величин X и Y и коэффициент корреляции равен …
Математическое ожидание случайной величины Х равна 5:M(X)=5. Чему равно значение математического ожидания М(-2Х)? По заданию ППЗ № 1 Тема № 5)
Установите соответствие между характеристикой случайной величины и ее формулойУстановите соответствие между характеристикой случайной величины и ее формулой (По заданию ППЗ № 1 Тема № 5)
Установите соответствие между характеристикой случайной величины и ее смысловым содержанием.
Инвестиционная компания предлагает для инвестиций два портфеля акций, каждый из которых содержит акции трех различных фирм. Согласно экспертной оценке, ожидаемая годовая прибыль акций первого портфеля составит:
- 5 тыс. долл. с вероятностью 0,5 (для акций первой фирмы);
- 10 тыс. долл. с вероятностью 0,2 (для акций второй фирмы); и
- 3 тыс. долл. с веро¬ятностью 0,3 (для акций третьей фирмы).
Для второго портфеля акций прогноз таков:
5,5 тыс. долл. — с вероятностью 0,6 (для акций первой фирмы);
5 тыс. долл. — с вероятностью 0,3 (для акций второй фирмы); и
6,5 тыс. долл. — с вероятностью 0,1 (для акций третьей фирмы).
Необходимо:
1) Построить законы распределения ожидаемого дохода акций каждого портфеля;
2) Оценить математическое ожидание годового дохода портфельных инвестиций;
3) Сделать вывод о направлении вложений.
Более высокий доход ожидается от акций портфеля …
Инвестиционная компания предлагает для инвестиций два портфеля акций, каждый из которых содержит акции трех различных фирм.
Согласно экспертной оценке, ожидаемая годовая прибыль акций первого портфеля составит: - 5 тыс. долл. с вероятностью 0,5 (для акций первой фирмы); - 10 тыс. долл. с вероятностью 0,2 (для акций второй фирмы); и - 3 тыс. долл. с вероятностью 0,3 (для акций третьей фирмы).
Для второго портфеля акций прогноз таков: 5,5 тыс. долл. — с вероятностью 0,6 (для акций первой фирмы); 5 тыс. долл. — с вероятностью 0,3 (для акций второй фирмы); и 6,5 тыс. долл. — с вероятностью 0,1 (для акций третьей фирмы).
Необходимо:
1) Построить законы распределения ожидаемого дохода акций каждого портфеля;
2) Оценить математическое ожидание годового дохода портфельных инвестиций;
3) Сделать вывод о направлении вложений.
(По заданию ППЗ № 5 Тема № 9)
Более высокий доход ожидается от акций портфеля …
Впишите 1 или 2
Предприниматель размышляет над тем, куда лучше вложить деньги: в акции компании 1 или акции компании 2. Согласно экспертной оценке, ожидаемая годовая прибыль от вложения средств в акции компании 1 составит:
- 5 тыс. долл. с вероятностью 0,5;
- 10 тыс. долл. с вероятностью 0,2; и
- 3 тыс. долл. с веро¬ятностью 0,3
Для акций компании 2 прогноз таков:
5,5 тыс. долл. — с вероятностью 0,6;
5 тыс. долл. — с вероятностью 0,3; и
6,5 тыс. долл. — с вероятностью 0,1.
Необходимо:
1) Построить законы распределения ожидаемого дохода для акций обеих компаний
2) Оценить математическое ожидание годового дохода от акций компании 1 и 2
3) Сделать вывод о направлении вложений.
Более высокий доход ожидается от акций компании …
Расположите указанные распределения в порядке ВОЗРАСТАНИЯ их математического ожидания (По заданию ППЗ № 8 Тема № 4)
Начало формыРасположите указанные распределения в порядке УБЫВАНИЯ их математического ожидания (По заданию ППЗ № 6 Тема № 4)
Начало формыРасположите указанные распределения в порядке возрастания их математического ожидания
Начало формыКонец формы
Впишите недостающие слова в название событий (со строчной буквы):
1. Событие называется __________ (обозначается буквой Ω), если в результате испытания оно обязательно должно произойти;
2. Событие называется __________ (обозначается буквой Ø), если в результате испытания оно не может произойти;
3. Два несовместных события, из которых одно должно обязательно произойти называются __________(По заданию ППЗ № 1 Тема № 3)Впишите недостающие слова в название применяемых на практике средних величин, применяемых в статистическом анализе (со строчной буквы):
1. Средней __________ вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот;
2. __________ вариационного ряда определяет значение признака, приходящегося на середину ранжированного ряда наблюдений;
3. __________ вариационного ряда определяет вариант, которому соответствует наибольшая частота.Впишите недостающие слова в название событий (со строчной буквы):
1. Два события называются __________ если появление одного из них не влияет на вероятность появления другого;
2. Два события называются __________ если появление одного из них исключает появления другого;
3. Два несовместных события, из которых одно должно обязательно произойти называются __________ (По заданию ППЗ № 2 Тема № 3)Случайная величина X имеет математическое ожидание М(X)=3. Установите соответствие между случайными величинами:
Y=2X+5; Z=3X-6; L= X+5
и значением их математических ожиданий.
D(Y) а) 3
D(Z) б) 8
D(L) в) 11Мода вариационного ряда 2, 3, 3, 5, 5, 5, 8, 8, 11, 12 равна…
Случайная величина X имеет дисперсию D(X)=3. Установите соответствие между случайными величинами:
Y=2X+5; Z=3X-6; L=X+24
и значением их дисперсий.
D(Y) а) 27
D(Z) б) 12
D(L) в) 3Дан доверительный интервал (10, 64; 12,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …
Дан доверительный интервал (6,02; 10,28) для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
Правосторонняя критическая область может определяться из соотношения …
Дисперсия случайной величины Х равна 5. Чему равно значение дисперсии D(X-1)
По многолетним статистическим данным, известно, что вероятность рождения мальчика равна 0,515. Для семьи, имеющей 4 ребенка определите …
1. Распределение, которое описывает вероятность числа детей мужского пола в этой семье;
2. Вероятность того, среди детей этой семьи нет мальчиков (только девочки).
3. Вероятность того, что все дети этой семьи – мальчики.
4. Наиболее вероятное число детей мужского пола в этой семье.
Наиболее вероятное число детей мужского пола в рассматриваемой семье равно …
Установите соответствие случайными величинами и значением их математических ожиданий.
1. M(X) а) 1,5
2. M(Y) б) 1,7
3. M(Z) в) 1,8Статистическое распределение выборки имеет вид:
Тогда значение относительной частоты
Статистическое распределение выборки имеет вид:
Тогда объем выборки равен
Дан доверительный интервал (26,06; 35,18) для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
Соотношением вида Р(К < -12,09) = 0,025 можно определить …
Пусть А – случайное событие, вероятность которого отлична от нуля и единицы. Расположите в порядке возрастания следующие вероятности. (По заданию ППЗ № 1 Тема № 3)
Установить последовательность ответов (По заданию ППЗ № 7 Тема № 3)
Чему равна дисперсия разности D(X-Y) двух независимых случайных величин X и Y, если известны значения дисперсий каждой из них: D(X)=3 и D(Y)=4? (По заданию ППЗ № 1
Тема № 5)
Задача: «В магазин вошло 500 покупателей. Найдите вероятность того, что 44 из них совершат покупки, если вероятность совершить покупку для каждого из них равна 0,7» решается с использованием локальной теоремы Лапласа, где аргумент у функции Лапласа находится по формуле (По заданию ППЗ № 9 Тема № 4)
20! не делится на число_____. (По заданию ППЗ № 1 Тема № 2)
В партии из 2500 семян подсолнечника 50 семян не взошли. Относительная частота появления невсхожих семян равна________. (По заданию ППЗ № 2 Тема № 1)
Из восьми карандашей различного цвета можно выбрать четыре карандаша ________способами? (По заданию ППЗ № 7 Тема № 2)
Четыре человека могут разместиться в салоне автобуса на четырех местах _________ способами. (По заданию ППЗ № 5 Тема № 2)
30! не делится на число _________. (По заданию ППЗ № 2 Тема № 2)
Число сочетаний
В партии из 500 деталей отдел технического контроля обнаружил 7 нестандартных деталей. Относительная частота появления нестандартных деталей равна______. (По заданию ППЗ № 2 Тема № 1)
Число размещений
Каковы причины использования асимптотических приближений формулы Бернулли? (По заданию ППЗ № 6 Тема № 4)
Монета бросается три раза. Какова вероятность Р выпадения подряд трех гербов? (По заданию ППЗ № 2 Тема № 3)
Различаются ли понятия "перестановки из трех элементов" и "размещения из трех элементов по три"? (По заданию ППЗ № 3 Тема № 2)
В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии. Всего партий было сыграно __________. (По заданию ППЗ № 3 Тема № 2)
Пусть А - случайное событие, вероятность которого - Р(А)=0,3. Чему равна вероятность события Р(А+А)? (По заданию ППЗ № 2 Тема № 3)
Дискретная случайная величина Х имеет биноминальный закон распределения с параметрами n и P. Укажите по какой формуле вычисляется дисперсия D(X). (По заданию ППЗ № 1 Тема № 5)
Вариантов выбора двух чисел из шести________способов. (По заданию ППЗ № 6 Тема № 2)
Пусть А - случайное событие, вероятность которого - Р(А)=0,3. Чему равна вероятность произведения событий Р(А*А)? (По заданию ППЗ № 4 Тема № 3)
Охарактеризуйте событие:
2х2=5 (По заданию ППЗ № 2 Тема № 1)
Впишите недостающие слова в название применяемых на практике средних величин, применяемых в статистическом анализе (со строчной буквы):
1. Средней __________ вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот;
2. __________ вариационного ряда определяет значение признака, приходящегося на середину ранжированного ряда наблюдений;
3. __________ вариационного ряда определяет вариант, которому соответствует наибольшая частота. (По заданию ППЗ № 4 Тема № 8)Впишите недостающие слова в название событий (со строчной буквы):
1. Два события называются __________ если появление одного из них не влияет на вероятность появления другого;
2. Два события называются __________ если появление одного из них исключает появления другого;
3. Два несовместных события, из которых одно должно обязательно произойти называются __________ (По заданию ППЗ № 2 Тема № 3)Размах варьирования вариационного ряда –1, 0, 2, 3, 4, 5, 7, 8, 10, 12, 14 равен … (По заданию ППЗ № 4 Тема № 9)
Найти математическое ожидание дискретной случайной величины Х, заданной следующим законом распределения (По заданию ППЗ № 8 Тема № 5)Чему равно математическое ожидание M(X+Y) суммы двух случайных величин X и Y,а если известны значения математических ожиданий каждой из них:M(X)=3; M(Y)=4? (По заданию ППЗ № 1 Тема № 5)
Математическое ожидание случайной величины Х равна 5:M(X)=5. Чему равно значение математического ожидания М(-2Х)? По заданию ППЗ № 1 Тема № 5)
Чему равно значение дисперсии числа 5? (По заданию ППЗ № 7
Тема № 5)
Дисперсия случайной величины Х равна 5. Чему равно значение дисперсии D(X-1) (По заданию ППЗ № 1 Тема № 5)
Вероятность того, что при бросании игрального кубика выпадет более 4 очков равна__________. (По заданию ППЗ № 7 Тема № 2)
Трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 без повторений цифр________. (По заданию ППЗ № 4 Тема № 2)
На рисунке представлены графики нормальных распределений N1, N2, N3. Расположите эти распределения в порядке возрастания их математического ожидания. (По заданию ППЗ № 5
Тема № 7)
Число размещений
Число сочетаний
Три человека в четырехместном купе на свободных местах могут разместиться _______ способами. (По заданию ППЗ № 8 Тема № 2)
В шашечном турнире участвуют 8 человек. Каждый из них сыграл с каждым по одной партии. Всего партий было сыграно________. (По заданию ППЗ № 8 Тема № 2)
Выбор двух чисел из четырех можно осуществить ________способами.
(По заданию ППЗ № 6 Тема № 2)
Вероятность того, что при бросании игрального кубика выпадет менее 4 очков равна_________. (По заданию ППЗ № 4 Тема № 1)
Из цифр 1,2,3,4,5 без повторений цифр можно составить ______ трехзначных чисел. (По заданию ППЗ № 3 Тема № 2)
Для нахождения вероятности того, что при 200 бросаниях игральной кости три очка появятся от 100 до 150 раз, используется (По заданию ППЗ № 8 Тема № 4)
Из цифр 1, 2, 3, 4, 5 без повторений цифр можно составить _______пятизначных чисел. (По заданию ППЗ № 3 Тема № 2)
- Установить последовательность ответов
Мы, ни раз, сдавали тесты по данному предмету и уверенно можем сказать: "Сделаем тест на хороший балл". Результаты сдачи, данного предмета, можете посмотреть во вкладке "Результаты"
Если необходима помощь, доверьте выполнения теста нам, так как, мы знакомы с Вашей системой тестирования.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)

- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.

2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:

- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


