-
ВЫ СТУДЕНТ ММУ (Московский Международный Университет)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Статистический метод контроля (1-1) ММУ
О НАС
Меня зовут Сергей, 8 лет я решаю тесты и пишу работы по данному предмету для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
Курсовая работа
НАПИШЕМ КУРСОВУЮ, НА ЛЮБУЮ ТЕМУ ПО ДАННОМУ ПРЕДМЕТУ.
Для уточнения стоимости и заказа работы, напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ.
Мы знакомы с требованиями для курсовых работ по данному предмету.
Выполняем работу полностью (текст, титульны, антиплагиат), при необходимости сами загружаем и контролируем выставление оценки.
Заказав работу у нас, Вам не нужно ни чего делать и дорабатывать.
Контрольная работа
ВЫПОЛНИМ ПРАКТИЧЕСКУЮ (СЕМИНАР) ПО ДАННОМУ ПРЕДМЕТУ.
С 01.09.2019 г. практические работы стали обязательными в ММУ, не выполнив практическую, не получите положительную оценку, даже если сдадите тесты на 5 баллов.
Закажите работу прямо сейчас и получите полностью оформленную работу, мы можем самостоятельно загрузить работу в личный кабинет и проконтролировать выставление оценки.
Для уточнения стоимости и заказа работы, напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ.
Ответы на тесты ММУ
РЕШИМ ТЕСТ ММУ НА ХОРОШУЮ ОЦЕНКУ.
Решаем тесты, для этого вуза, более 5 лет. Знаем все требования и процедуру сдачи. Закажите решение теста по данному предмету и получите хорошую оценку, работаем самостоятельно, не нанимаем сторонних лиц, поэтому конфиденциальность гарантируем.
Напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ. И В КАЧЕСТВЕ ТЕСТА НАШИХ УСЛУГ, ПЕРВЫЙ ТЕСТ СДАДИМ БЕСПЛАТНО (тест сдается бесплатно, если ранее ни чего у нас не заказывали, проверка по логину).
Результаты наших решений, можете посмотреть во вкладке "РЕЗУЛЬТАТЫ".
Тестирование проходит на официальном сайте ММУ в личном кабинете ЭИОС https://elearn.interun.ru.
Оценка выставляется, по лучшему результату.
ВОПРОСЫ ТЕСТА ММУ ПО ДАННОМУ ПРЕДМЕТУ:
Что полностью характеризует случайную величину:
Чему равна вероятность случайного события:
Что называют средним квадратическим отклонением случайной величины:
Как обозначают вероятность события А:
Чему равна вероятность достоверного события:
Какой формулой определяется относительная частота события А:
Чему равна дисперсия разности двух независимых случайных величин:
Как принято обозначать случайные события:
Что называют условной вероятностью:
Когда вычисляют относительную частоту:
Какие значения случайная величина X может принимать в одном испытании:
Как обозначают условную вероятность:
Сколько значений может принять случайная величина в результате испытания:
Какие бывают элементарные исходы:
Чему равна вероятность совместного появления нескольких событий, независимых в совокупности:
Если одно из двух противоположных событий обозначено через А, то как принято обозначать другое:
Какая вероятность появления одного из двух несовместных событий А и В, безразлично какого:
Когда вычисляют вероятность события:
Чему равно математическое ожидание дискретной случайной величины:
Что необходимо для задания дискретной случайной величины:
Какое значение имеет математическое ожидание постоянной величины М(С) :
Чему равно математическое ожидание постоянной величины С:
Какие события называют несовместными:
Каким может быть число возможных значений непрерывной случайной величины:
Какое неравенство доказал Чебышев:
По какому равенству находят выравнивающие частоты:
Какая вероятность того, что непрерывная случай¬ная величина примет значение, принадлежащее интер¬валу (а, b) :
Какая вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения:
Что называют статистическим распределением выборки:
Какое нормальное распределе¬ние называют общим:
Что называют полигоном частот:
Чем задается дискретная случайная величина:
Чему равно среднее квадратическое отклонение случайной величины X:
Как, зная плотность распределения f (x), можно найти функцию распределения F (х) :
По какой формуле зная плотность распределения можно найти функцию распределения:
Какие значения интегральной функции принад¬лежат отрезку [0; 1] :
Что необходимо знать, чтобы задать нормальное распределение:
Если возможные значения непрерывной случайной величины расположены по всей оси х, то при lim x →∞ F (X) :{
Какую статистическую ошибку Θ* при любом объеме выборки называют несмещенной:
Какую статистическую оценку называют состоятельной:
По какому равенству находят выравнивающие частоты:
Какое геометрическое истолкование функции распределения:
Какое распределение вероятностей называют равномерным:
Чему равно среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин:
Какое нормальное распределение называют нормированным:
Какой оценкой генеральной средней является выборочная средняя:
При каком эксцессе кривая распределения имеет более низкую и “плоскую” вершину, чем нормальная кривая:
Какой вид имеет график дифференциальной функции равномерного распределения:
При каком эксцессе кривая распределения имеет более высокую и “острую” вершину, чем нормальная кривая:
Какая функция является общим способом задания любых типов случайных величин:
Чему равна интегральная функция нормированного нормального распределения F0(x) :
Чему равна дискретная генеральная средняя совокупность относительно количественного признака X:
Какими оценками при небольшом объеме выборки следует пользоваться:
Что в теории вероятностей понимают под распределением:
Что называют гистограммой частот:
Чему равна вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b) :
Как на практике правило трех сигм:
Соблюдение каких требований гарантирует математическое ожидание оценки Θ* от получения систематических ошибок:
Какой вид имеет график дифференциальной функции дискретного распределения:
Какую функцию называют интегральной функцией распределения:
Какой вид отбора не требует расчленения генеральной совокупности на части:
Какие соотношения μ 1связывают начальные v1 и центральные v2 моменты:
Какую функцию называют функцией распределения:
Как называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру:
Для каких случайных величин справедливо неравенство Чебышева:
По какой формуле определяют условные варианты:
В чем состоит сущность правила трех сигм:
Чему равна сумма вероятностей возможных значений дискретной величины заданной таблично:
Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
Задано распределение частот выборки. Найти объем выборки.
Чему равна вероятность того, что непрерывная случайная величина Х примет одно определенное значение:
Дисперсия каждой из 9 одинаково распределенных взаимно независимых случайных величин равна 36. Найти дисперсию среднего арифметического этих величин.
(вид отв. х)
Что геометрически означает свойство “ Дифференциальная функция неотрицательна”:
Выберите один ответ.
Что не называют числовой характеристикой случайной величины:
Чему равна вероятность совместного появления двух независимых событий А и В:
Чему равен несобственный интеграл от дифференциальной функции :
События А, В, С и D образуют полную группу. Вероятность событий такова: Р (А) = 0,1; Р (B) = 0,4; Р (C) = 0,3. Чему равна вероятность события D?
(вид отв. х , х):
Случайная величина X задана интегральной функцией
Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (2; 3).
Найти условную варианту u3 статистического распределения
По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Определите относительную частоту поражения цели.
(вид отв. хx / хх)
Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей.
(вид отв. х , хх)
Найти общую среднюю ¯x совокупности, состоящей из двух групп
Выбрать варианту в качестве ложного нуля следующего статистического распределения:
Какая из теорем является простейшим законом больших чисел:
Какой эмпирический момент определяют по формуле :
Какая выборка будет репрезентативной:
Чему равна дифференциальная функция φ(x) нормированного распределения:
Если возможные значения непрерывной случайной величины расположены по всей оси х, то при lim x →-∞ F (X) :{
Чему равна вероятность появления хотя бы одного из двух несовместных событий А и В:
Чему равна вероятность совместного появления двух зависимых событий А и В:
Чему равна вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1,B 2образующих полную группу:
Чему равна дисперсия суммы постоянной величины и случайной:
Чему равна дисперсия числа появлений события в независимых испытаниях:
Как обозначают математическое ожидание дискретной случайной величины:
Чему равна вероятность появления хотя бы одного из двух независимых событий А и В:
Как принято обозначать среднее квадратичное отклонение случайной величины:
Чему равна вероятность появления хотя бы одного из двух совместных событий А и В:
Какая формула для вычисления дисперсии (рассеяния) дискретной случайной величины:
Когда событие А и В называют независимыми:
Какое неравенство удовлетворяет вероятность любого события:
Чему равно математическое ожидание М (Х) числа появлений события А в n независимых испытаниях:
Какие события называют противоположными:
Что называют элементарным исходом:
Как принято обозначать случайные величины:
Как обозначают дисперсию (рассеяние) дискретной случайной величины:
Что называют полной группой событий:
Чему равен несобственный интеграл от плотности распределения :
Чему равна интегральная функция общего нормального распределения F(x) :
Какая вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение:
Какую из функций можно найти, зная плотность распределения:
Какому интервалу принадлежат значения функции распределения:
Какое нормальное распределение называют нормированным:
Чему равна сумма произведений отклонений на соответствующие частоты :
Чему равна сумма вероятностей противоположных событий A и A ?:
Как можно выносить за знак дисперсии D(СX) постоянный множитель:
Какая вероятность появления одного из двух несовместных событий А и В:
Какие два события называют независимыми:
Каким может быть число возможных значений дискретной случайной величины:
Как называют статистическую оценку, которая при n>? стремится по вероятности к оцениваемому параметру:
Чему равен несобственный интеграл от дифференциальной функции :
Какой эмпирический момент определяют по формуле :
В каком случае функция F (х) — неубывающая:
Если возможные значения непрерывной случайной величины расположены по всей оси х, то при lim x >? F (X) :{
Случайная величина задана законом распределения
Найти среднее квадратическое отклонение этой величины.
В денежно - вещевой лотерее на каждые 10 000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?
Найти групповые средние ?x1 и ?x2 совокупности, состоящей из двух групп
Дано: Р (|Х — М (Х)|< е) > 0,9; D (X) = 0,004. Пользуясь неравенством Чебышева, найти ?.
Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, при чем вероятность выигрыша по одному билету равна 0,3.
Какие соотношения ? 1связывают начальные v1 и центральные v2 моменты:
Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
Найти дисперсию случайной величины, зная закон ее распределения
Производится 4 выстрела с вероятностями попадания в цель р1 = о,6, p2 = 0,4, p3 = 0,5 и р4 = 0.7. Найти математическое ожидание общего числа попаданий.
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2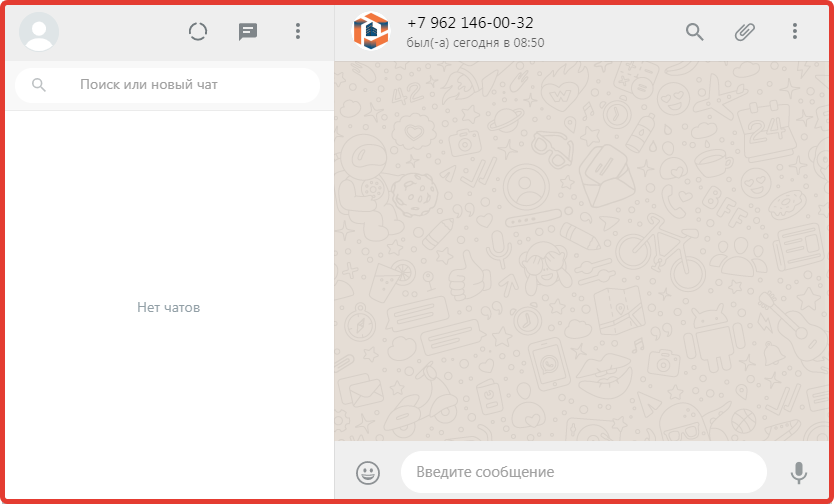
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3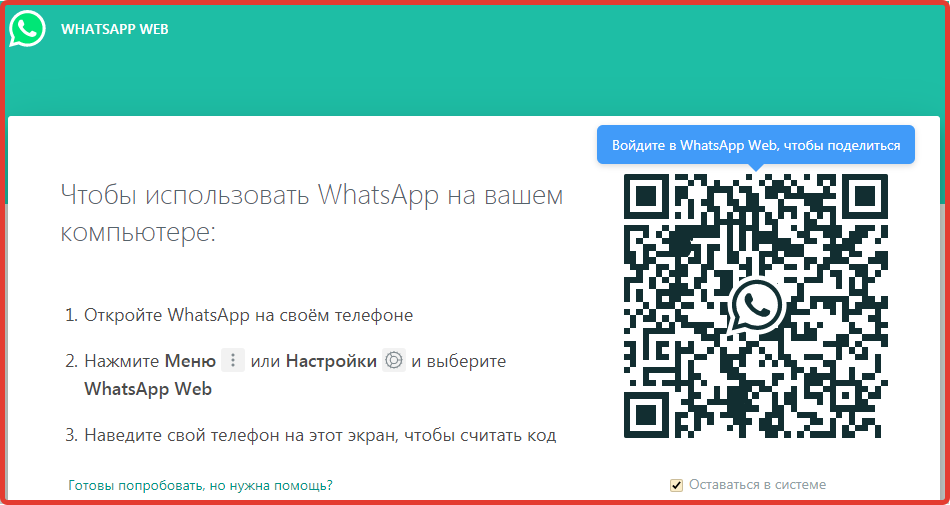
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
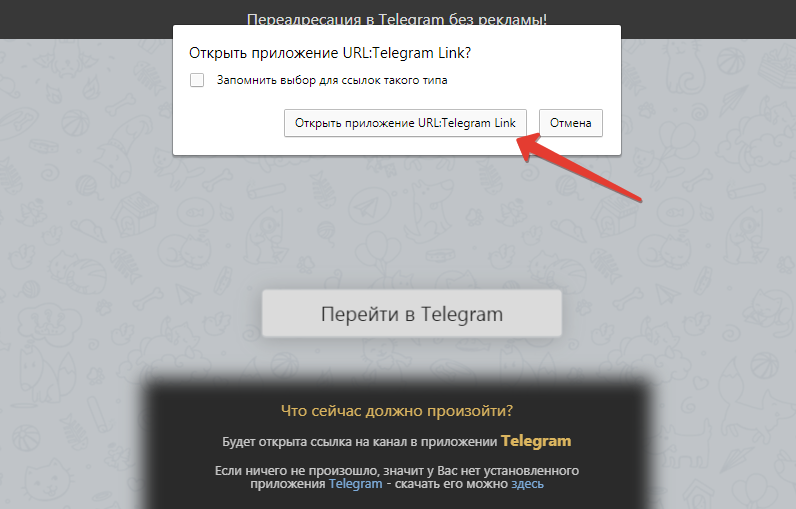
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


