-
ВЫ СТУДЕНТ МИЭП (Международный Институт Экономики и Права)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Математический анализ МИЭП
О НАС
Меня зовут Сергей, 10 лет я решаю тесты и пишу работы по данному предмету, для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Высокий процент сдачи тестов.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2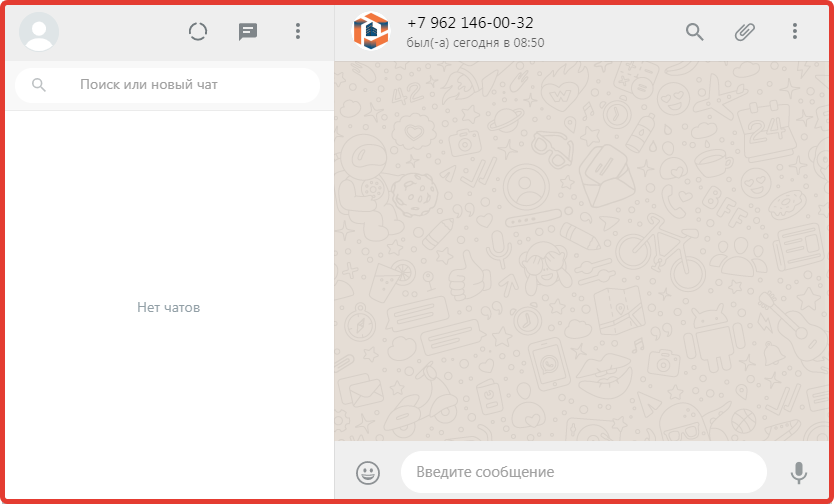
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3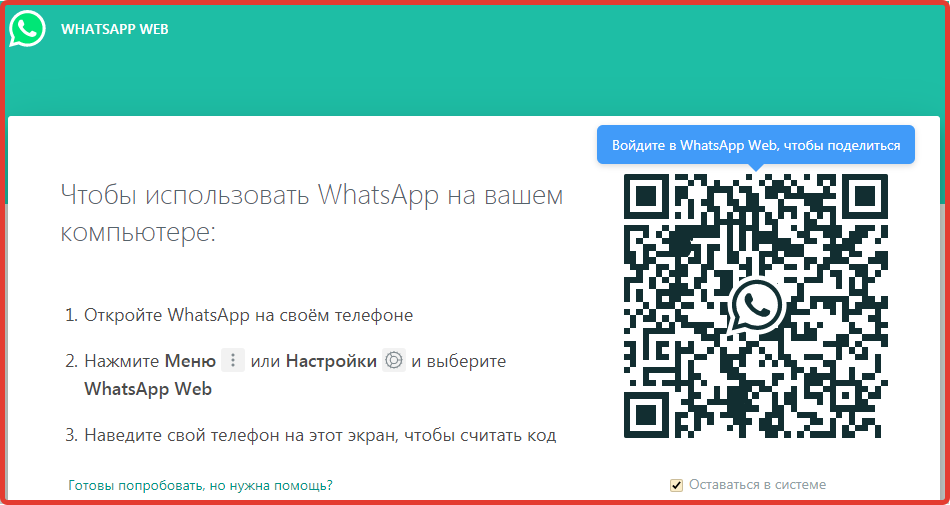
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:
Курсовая работа
По данному предмету, данный вид работы не предусмотрен.
Мы, ни раз, писали КР (курсовые работы) по данному предмету и уверенно можем сказать: "Сделаем по всем требованиям". Вам останется только сдать работу, пишем работу полностью, оформляем, вставляем титульный лист, все работы проверям на антиплагиат, если будут замечания исправляем бесплатно.
Если необходима помощь, доверьте написания КР нам, так как, мы знакомы с требованиями Вашего ВУЗа, работаем профессионально и оперативно.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Ответы на тесты МИЭП
Тестирование проходит на официальном сайте МИЭП http://sdo1.miep.ru и http://sdo.miep.ru Оценка выставляется, по первому положительному результату.
Вопросы для подготовки к тестированию:
-
Какое из следующих свойств дифференциала функции сформулировано неверно
Предел функции.
(ПТК: тема 3, задание 1)
Предел функции.
(ПТК: тема 4, задание 2)
Предел функции.
(ПТК: тема 3, задание 1)Предел функции.
(ПТК: тема 4, задание 2)
Предел
Какую из перечисленных функций можно определить как сложную?
Какая из следующих функций является четной?
Вопрос: Какая из следующих функций не является нечетной? (Вес: 1)
Вопрос: Какую из перечисленных функций можно определить как сложную? (Вес: 1)
Какую из перечисленных функций можно определить как сложную? (Вес: 1)
Какое из следующих утверждений выполняется для функции y=sinx
Значение предела равно
(ПТК: тема 4, задание 4)
Значение предела равно
(ПТК: тема 4, задание 2)
Значение предела равно
(ПТК: тема 4, задание 4)
Какую из перечисленных функций можно определить как сложную? (Вес: 1)
Вопрос: Найти предел (Вес: 1)
Вопрос: Найти предел (Вес: 1)
Вопрос: Если функция непрерывна в точке x=a,то какое из перечисленных условий неверно? (Вес: 1)Конец формы
Функция является вогнутой на данном интервале, если на этом интервале (ПТК: тема 5, задание 11)
Какое из следующих правил дифференцирования записано неверно?
Начало формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыКакую из перечисленных функций можно определить как сложную?
Начало формы
Найти предел
Конец формыНачало формы
Расположите пределы в порядке возрастания их величины
Конец формыКонец формы
Какую из перечисленных функций можно определить как сложную?
Функция будет непрерывной при а равном (ПТК: тема 4, задание 6)
Горизонтальная асимптота графика функции
(ПТК: тема 8, задание 1)
Какая из следующих форм используется для определения необходимого условия экстремума функции?
Начало формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыНачало формы
Найти предел
Конец формыЕсли функция непрерывна в точке x=a,то какое из перечисленных условий неверно?
Начало формыНайти предел
Конец формы
Какое из следующих условий характеризует убывание функции на интервале?
Конец формыНачало формы
Даны графики прямых f,g,h,u. Укажите последовательность этих прямых в порядке возрастания их угловых коэффициетов
Конец формыНачало формы
На рисунке представлены графики линейных функций f,g,h,u. Укажите последовательность этих прямых в порядке убывания их производных
Конец формыМаксимум функции равен
(ПТК: тема 6, задание 3)
Начало формыФункция y=f(x) определена на промежутке (-5;4). На рисунке изображен график ее производной.Тогда точкой минимума функции y=f(x) определена на промежутке (-5;4) является точка х=...
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Начало формыТочкой разрыва
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыКакое из следующих условий характеризует возрастание функции на интервале?
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыЧто характеризует вторая производная функции?
Начало формыКакое из следующих приложений не имеет отношения к понятию первой производной функции?
Какая из следующих формул используется для определения необходимого условия перегиба функции в точке?
Начало формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Начало формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Конец формыКонец формы
Выбор единственно правильного ответа
Укажите правильный результат для разности пересекающихся множеств А. Это:
Какая из следующих прямых параллельна прямой у = 4х-15?
Какую из перечисленных функций можно определить как сложную?
Заданы две прямые: у = ax + b и у = cx + d. При каком условии эти прямые
перпендикулярны?
Какое из следующих утверждений выполняется для функции y = sin x?
Какая из следующих функций является четной?
Для системы из двух линейных уравнений подсчитаны определители: D = 0, D(x) = 0, D(y)
= 0. Эта система:
Для произведения двух квадратных матриц получено АВ = А. Следовательно, матрица В
по отношению к А является:
На плоскости заданы три вектора А, В и С. Вектор С может быть представлен линейной
комбинацией векторов А и В:
Какое из следующих приложений не имеет отношения к понятию первой производной
функции?
Дифференциал функции - это:
Если функция непрерывна в точке х = а, то какое из перечисленных условий неверно?
Какое из следующих правил дифференцирования записано неверно?
Что характеризует вторая производная функции?
Какое из следующих свойств дифференциала функции сформулировано неверно?
Какая из следующих формул используется для определения необходимого условия перегиба функции в точке?
Какое из следующих условий характеризует убывание функции на интервале?
Какое из следующих условий обеспечивает максимальное значение функции в стационарной точке?
Функция является вогнутой на данном интервале, если на этом интервале:
Множество содержит четыре элемента. Сколько подмножеств можно образовать для
этого множества?
Укажите правильный результат для разности пересекающихся множеств В. Это:
Какая из следующих прямых перпендикулярна прямой у = 4х-15?
Какую из перечисленных функций можно определить как сложную?
Заданы две прямые: y = ax + b и у = cx + d. При каком условии эти прямые
параллельны?
Какое из следующих утверждений не выполняется для функции y = ln x?
Какая из следующих функций не является нечетной?
Для системы из двух линейных уравнений подсчитаны определители: D = 0, D(x) = 20,
D(y) = 10. Эта система:
Для произведения двух квадратных матриц получено АВ = Е. Следовательно, матрица
В по отношению к А является:
Какая из следующих формул используется для определения необходимого условия экстремума функции?
Два множества A и B заданы свойствами:
Вычислить следующий определитель:
Какую из перечисленных функций можно определить как сложную?
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
39. Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Среди перечисленных вариантов укажите все правильные производные для функции
f(x):
Определить скалярное произведение следующих двух векторов:
Определить скалярное произведение следующих двух векторов:
Определить скалярное произведение следующих двух векторов:
Определить длину следующего вектора:
Определить длину следующего вектора:
Определить длину следующего вектора:
Найти предел:
Найти предел:
Найти предел:
Значение предела равно
(ПТК: тема 4, задание 4)
Найти предел:
Найти предел:
Найти предел:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Вычислить следующий определитель:
Вычислить следующий определитель:
Вычислить следующий определитель:
Предел алгебраической суммы конечного числа функций определяется
Если первая производная функции y=f(x) на интервале x1 < x < x2 больше нуля, а
вторая меньше нуля, то крутизна касательной к графику функции в текущей точке x
Какая из следующих прямых параллельна прямой у = 4х-15?
Какую из перечисленных функций можно определить как сложную?
Заданы две прямые: у = ax + b и у = cx + d. При каком условии эти прямые
перпендикулярны?
Какое из следующих утверждений выполняется для функции y = sin x?
Найти предел:
Для системы из двух линейных уравнений подсчитаны определители: D = 0, D(x) = 0, D(y)
= 0. Эта система:
Для произведения двух квадратных матриц получено АВ = А. Cледовательно, матрица В
по отношению к А является:
На плоскости заданы три вектора А, В и С. Вектор С может быть представлен линейной
комбинацией векторов А и В:
Какое из следующих приложений не имеет отношения к понятию первой производной
функции?
Дифференциал функции - это:
Если функция непрерывна в точке х = а, то какое из перечисленных условий неверно?
Какое из следующих правил дифференцирования записано неверно?
Что характеризует вторая производная функции?
Какое из следующих свойств дифференциала функции сформулировано неверно?
Какая из следующих формул используется для определения необходимого условия
перегиба функции в точке?
Какое из следующих условий характеризует убывание функции на интервале?
Какое из следующих условий обеспечивает максимальное значение функции в
стационарной точке?
Функция является вогнутой на данном интервале, если на этом интервале:
Вычислить следующий определитель:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Какая из следующих прямых перпендикулярна прямой у = 4х-15?
Какую из перечисленных функций можно определить как сложную?
Заданы две прямые: y = ax + b и у = cx + d. При каком условии эти прямые
параллельны?
Какое из следующих утверждений не выполняется для функции y = ln x?
Какая из следующих функций не является нечетной?
Для системы из двух линейных уравнений подсчитаны определители: D = 0, D(x) = 20,
D(y) = 10. Эта система:
Для произведения двух квадратных матриц получено АВ = Е. Следовательно, матрица
В по отношению к А является:
Какая из следующих формул используется для определения необходимого условия
экстремума функции?
Два множества A и B заданы свойствами:
Для вычисления предела дробно-рациональной функции в случае неопределенности
типа (0/0) необходимо
Какую из перечисленных функций можно определить как сложную?
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Среди перечисленных вариантов укажите все правильные производные для функции
f(x)
Определить скалярное произведение следующих двух векторов:
Определить скалярное произведение следующих двух векторов:
Определить скалярное произведение следующих двух векторов:
Определить длину следующего вектора:
Определить длину следующего вектора:
Какая из следующих функций является четной?
Определить длину следующего вектора:
Вычислить следующий определитель:
Найти предел:
Найти предел:
Найти предел:
Найти предел:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Среди матриц B, C и D найдите матрицу обратную матрице A, если:
Вычислить следующий определитель:
Даны два множества
Даны два множестваДаны два множества
Конец формы
Даны два множестваДаны два множества
Начало формыДаны два множестваФункция у=e^x...
Функция у=e^x...
функция y=x^2...
Функция y=x2 …Конец формыНачало формы
Конец формы
Функция y=ex …
Множество решений неравенства определяется выражением …
Начало формыКонец формы
Начало формы
Функция y=x3 …Конец формы
функция у=х^3...
Вторая производная дважды дифференцируемой функции в точке перегибаУстановите соответствие между типом множества и его принятым обозначением
1. R а) множество натуральных чисел
2. Z б) множество действительных чисел
3. N в) множество целых чиселМножество решений неравенства определяется выражением …
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)ПОСЛЕ ИЗМЕНЕНИЯ:
Установите соответствие между понятиями производной, дифференциала функции, дифференциала аргумента и их условными обозначениями
(ПТК: тема 9, задание 1)Функция y=f(x) определена на промежутке (-5;4). На рисунке изображен график ее производной. Установите соответствие между указанными значениями аргумента х и наличием экстремума функции в этих точках.
(ПТК: тема 5, задание 13)
Функция y=f(x) определена на промежутке (-5;4). На рисунке изображен график ее производной.Тогда точкой минимума функции y=f(x) определена на промежутке (-5;4) является точка х= (ПТК: тема 5, задание 13)
Расположите пределы в порядке возрастания их величины
(ПТК: тема 4, задание 2)
Вертикальная асимптота графика функции
(ПТК: тема 8, задание 1)
Конец формыУстановите соответствие между типом множества и его принятым обозначением:
(ПТК: тема 1, задание 4)На рисунке представлены графики линейных функций f, g, h, u. Укажите последовательность этих прямых в порядке убывания их производных. (ПТК: тема 5, задание 13
Указанная ниже функция имеет разрывы в точках
(ПТК: тема 7, задание 1)
На рисунке представлены графики четырех функций. Охарактеризуйте непрерывность этих функций в точке х=0 (ПТК: тема 4, задание 7)
Расположите пределы в порядке убывания их величины
(ПТК: тема 4, задание 2)
Если функция непрерывна в точке x=a, то НЕВЕРНО условие
(ПТК: тема 4, задание 6)
Убывание функции на интервале характеризует условие (ПТК: тема 5, задание 13)
Отметьте НЕВЕРНО записанное правило дифференцирования
(ПТК: тема 5, задание 1)
Среди перечисленных ниже, сложной является функция
(ПТК: тема 2, задание 6)
Значение предела равно
(ПТК: тема 3, задание 1)
Для функции y=sinx выполняется утверждение
(ПТК: тема 2, задание 3)
Максимальное значение функции в стационарной точке обеспечивает условие (ПТК: тема 5, задание 13)
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Для определения необходимого условия экстремума функции используется форма (ПТК: тема 5, задание 13)
Выпуклость функции.
(ПТК: тема 7, задание 1)
Значение предела равно
(ПТК: тема 3, задание 1)
Выпуклость функции.
(ПТК: тема 7, задание 1)
Вторая производная функции характеризует (ПТК: тема 5, задание 11)
Среди перечисленных ниже, сложной является функция
(ПТК: тема 2, задание 6)
Начало формыСреди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Исследование функции.
(ПТК: тема 7, задание 2)
Исследование функции.
(ПТК: тема 8, задание 1)
Исследование функции.
(ПТК: тема 7, задание 1)
Исследование функции.
(ПТК: тема 8, задание 1)
Исследование функции.
(ПТК: тема 7, задание 1)
Исследование функции.
(ПТК: тема 7, задание 2)
Возрастание функции на интервале характеризует условие (ПТК: тема 5, задание 13)
Среди перечисленных ниже, сложной является функция
(ПТК: тема 2, задание 6)
Операции над множествами
(ПТК: тема 1, задание 4)
Выпуклость функции.
(ПТК: тема 7, задание 1)
Расположите указанные ниже функции f, g, h в порядке возрастания значений их первой производной в точке x=0.
(ПТК: тема 5, задание 1)
Указанная ниже функция имеет разрывы в точках
(ПТК: тема 7, задание 1)
Расположите указанные ниже функции f, g, h в порядке убывания значений их производных в точке x=0.
(ПТК: тема 5, задание 1)
Указанная ниже функция имеет разрывы в точках
(ПТК: тема 7, задание 1)
Глобальный максимум функции.
(ПТК: тема 7, задание 1)
Операции над множествами.
(ПТК: тема 1, задание 1)
Для определения необходимого условия перегиба функции в точке используется формула (ПТК: тема 5, задание 11)
Дифференциал функции характеризует (ПТК: тема 9, задание 10)
Эластичность Еx(y) функции y=f(x) вычисляется по формуле
(ПТК: тема 8, задание 2)
Среди перечисленных ниже, четной является функция
(ПТК: тема 2, задание 3)
Оценить множество.
(ПТК: тема 1, задание 6)
Значение предела равно
(ПТК: тема 3, задание 1)
Значение предела равно
(ПТК: тема 4, задание 4)
Исследование функции.
(ПТК: тема 8, задание 1)
Исследование функции.
(ПТК: тема 7, задание 2)
Установите соответствие между указанными ниже пределами и их числовыми значениями.
(ПТК: тема 4, задание 2)
Указанная ниже функция имеет разрывы в точках
(ПТК: тема 7, задание 1)
Установите соответствие между графиками функции и значениями ее первой и второй производной.
(ПТК: тема 1, задание 1)
Установите соответствие между указанными ниже пределами и их названиями.
(ПТК: тема 4, задание 2)
На рисунке представлены графики функций y(x), g(x) и h(x). Расположите эти функции в порядке убывания их второй производной в точке x=0.
(ПТК: тема 7, задание 2)
На рисунке представлены графики функций y(x), g(x) и h(x). Установите соответствие между второй производной этих функций и ее значением в точке x=0.
(ПТК: тема 7, задание 2)
Операции над множествами.
(ПТК: тема 1, задание 1)
Установите соответствие между указанными ниже функциями и их производными.
(ПТК: тема 5, задание 5)
Локальный максимум приведенной ниже функции достигается в точке
(ПТК: тема 6, задание 3)
Указанная ниже функция имеет разрывы в точках
(ПТК: тема 7, задание 1)
К понятию первой производной функции НЕ имеет отношения следующее приложение
(ПТК: тема 5, задание 13)
Операции над множествами
(ПТК: тема 1, задание 4)
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Выпуклость функции.
(ПТК: тема 7, задание 2)
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Среди перечисленных ниже, нечетной является функция
(ПТК: тема 2, задание 3)
Вторая производная функции характеризует
(ПТК: тема 7, задание 2)
Среди перечисленных вариантов укажите все правильные производные для функции f(x) (ПТК: тема 5, задание 1)
Операции над множествами
(ПТК: тема 1, задание 4)Разрыв функции.
(ПТК: тема 4, задание 6)
Производная функции имеет вид (ПТК: тема 6, задание 3)
Исследование функции.
(ПТК: тема 7, задание 2)
Исследование функции.
(ПТК: тема 7, задание 2)
Выпуклость функции.
(ПТК: тема 7, задание 1)
На рисунке представлены графики функций y(x), g(x) и h(x). Расположите эти функции в порядке возрастания их второй производной в точке x=0.
(ПТК: тема 7, задание 2)
На рисунке представлены графики линейных функций f, g, h, u. Укажите последовательность этих прямых в порядке возрастания их угловых коэффициентов.
(ПТК: тема 5, задание 13)
Установите соответствие между операциями над множествами и соответствующими им диаграммами Эйлера-Венна.
(ПТК: тема 1, задание 1)
Установите соответствие между знакопеременными рядами и видами сходимостиДля нахождения экстремума функции z=f(x,y) при условии g(x,y)=С используется функция Лагрнажа,определяемая
Начало формы
Для нахождения условного экстремума функции z=f(x,y)при условии g(x,y)=C используется функция Лагранжа определяемая как:
Конец формы
Вычислить значение частной производной функции z(x,y)по переменной у в точке (0,0)
Вычислите значение частной производной второго порядка функции z(x,y)по переменной у в точке (1,1)
Укажите порядок дифференциального уравнения
Укажите порядок дифференциального уравнения (цифра)
Начало формы
Что определяется выражением
Конец формы
Начало формы
Расположите определенные интегралы в порядке возрастания и числового значения
Вычислить значение частной производной функции z(x,y)по переменной у в точке (0,0)
Метод множителя Лагранжа используется для
Несобственный интеграл с бесконечным пределом интегрирования
Вычислить значение частной производной функции z(x,y) по переменной х в точке (0,0)
Расположите определенные интегралы в порядке возрастания их числового значения
Расположите определенные интегралы в порядке возрастания их числового значения
Конец формы
Начало формы
Установите соответствие между числовой последовательностью и формулой её общего члена
Установите соответствие между числовой последовательностью и формулой ее общего члена
Определить критические точки функции z(x,y)
Вычислить значение определенного интеграла
Установите соответствие между дифференциальным уравнением и его порядком
Конец формы
Вычислить значения определенного интеграла
Вычислить значение определенного интеграла
Укажите верное решение дифференциального уравнения
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Укажите тип дифференциального уравнения
Вычислить значение определенного интеграла
Конец формы
Начало формы
Вычислить значение определенного интеграла
Начало формы
Найти частную производную функции z(x,y)по переменной у
Конец формы
Начало формы
Найти частную производную функцию z(x,y)по переменной у
укажите верное значение интеграла
Найти частную производной функции z(x,y) по переменной x
Вычислить значение частной производной функции z(x,y) по переменной y в точке (0,0)
Укажите
верное решение дифференциального уравнения
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Укажите верное решение дифференциального уравнения.
Укажите верное значение интеграла.
Вычислить значение определенного интеграла
Вычислить значение определенного интеграла
Вычислить значение определенного интеграла
Вычислите значение определенного интеграла
Частная производная первого порядка функции двух переменных по своему физическому смыслу представляет
Укажите верное решение дифференциального уравнения
Укажите верное решение дифференциального уравнения
Вычислить значение несобственного интеграла
Производная от неопределенного интеграла равна
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Найти частную производной функции z(x,y) по переменной х в точке (0,0)
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Найти частную производную второго порядка функции z(x,y) по переменной x в точке (0,0)
Найти частную производную второго порядка функции z(x,y) по переменной x в точке (0,0)
Может ли быть положительной интегральная сумма отрицательной функции на отрезке?
Найти частную производную функции z(x,y) по переменной y в точке (0,0)
Найти частную производную функции z(x,y) по переменной y в точке (0,0)
Начало формы
Найти частную производную функции z(x,y) по переменной y
Найти частную производную функции z(x,y) по переменной y в точке (0,0)
Среди перечисленных выражений укажите правильное для следующего интеграла
Среди перечисленных выражений укажите правильно для следующего интеграла
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Нахождение частных решений дифференциальных уравнений по начальным условиям называется решением задачи
Предел интегральной суммы на отрезке [a,b],если максимальная длина интервала разбиения стремится к нулю равен
Что такое подыинтегральное выражение?
Что такое подынтегральное выражение?
Среди перечисленных ниже выражений укажите правильное для следующего интеграла: ∫dx / cos2x;
Градиент функции двух переменных-это
Вычислить значение частной производной функции z(x,y) по переменной y в точке (0,0)
Среди перечисленных ниже выражений укажите правильное для следующего интеграла: ∫dx / sin2x;
Метод множителей Лагранжа используется для
Среди перечисленных ниже выражений укажите правильное для следующего интеграла: ∫dx/a2+x2
Начало формы
Найти частную производную второго порядка функции z(x,y) по переменной x
Найти частную производную второго порядка функции z(x,y) по переменной y
Вычислить значение частной производной функции z(x,y) по переменной y в точке (0,0)
Как называется эта функция?
Определить критические точки функции z(x,y)= 25 - x^2 - y^2
Найти частную производную второго порядка функции z(x,y) по переменной x в точке (1,1)
Найти частную производную функции z(x,y) по переменной x в точке (0,0)
Укажите отличие двух различных первообразных одной и той же функции
Найти частную производной функции z(x,y) по переменной y
Объем произведенной продукции может быть найден
Производная от неопределенного интеграла равна
Укажите тип дифференциального уравнения
Определить критические точки функции z(x,y)
Производная определенного интеграла с постоянными пределами интегрирования равна
Найти частную производную функции z(x,y) по переменной x в точке (0,0)
Начало формы
Найти частную производную функции z(x,y) по переменной y.
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Укажите верное значение интеграла.
Укажите верное значение интеграла.
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Если величина градиента функции z(x,y) в данной точке отлична от нуля,то градиент
Укажите один из перечисленных ниже объектов, который не может быть результатом вычисления определенного интеграла от функции f(x) с постоянными пределами интегрирования
Найти частную производную второго порядка функции z(x,y) по переменной y.
Вычислить значение определенного интеграла
Вычислить значение несобственного интеграла
Найти частную производную второго порядка функции z(x,y) по переменной y в точке (1,1)
Найти частную производную второго порядка функции z(x,y) по переменной y в точке (1,1)
Найти частную производную второго порядка функции z(x,y) по переменной y в точке (1,1)
Вычислить значение определенного интеграла
Дано дифференциальное уравнение:
Укажите правильное значение интеграла
Вычислите значение определенного интеграла
Для функции y(x)=ex
Определите градиент функции f(x,y,z)=2x2+yz-18
Вычислите значение определенного интеграла
Начало формы
Вычислите значение определенного интеграла
Конец формы
Найти частную производную второго порядка функции z(x,y) по переменной x
Конец формы
Найти частную производную второго порядка функции z(x,y) по переменной x
Частная производная df/dx функции f(x,y)=15ln(x+y2) равна…
Для функции: z(x,y)=x3+8y3-6xy+5:
Общим решением дифференциального уравнения у"+9y=0 является функция …
Установите соответствие между дифференциальным уравнением и общим видом его частного решения.
Укажите правильное значение дифференциала от неопределенного интеграла
Расположите дифференциальные уравнения в по возрастанию их порядка
Расчет значений "неберущихся" интегралов
Данное выражение определяет
Укажите последовательность вычисления определенного интеграла
Первообразная для функции f(x)
Для указанных последовательностей укажите формулу общего члена
Вычислите модуль комплексного числа Z=4+3i:
|Z|=KДля комплексного числа Z=4+3i расположите указанные выражения в порядке возрастания их значений:
Укажите правильное значение интеграла
Определить критические точки функции z(x,y)
Определить критические точки функции z(x,y)= x + y
Общим решением дифференциального уравнения y"-3y’+2y=0 является функция
Установите соответствие между дифференциальным уравнением и его порядком
Вычислить значение несобственного интеграла
Значение частной производной df/dy функции f(x,y)=exy2 в точке А(0,2) равно …
Общим решением дифференциального уравнения y’’+9y=0 является функция …
Укажите правильное значение интеграла
Укажите отличие первообразной для функции f(x) и неопределенного интеграла от этой функции.
Укажите порядок дифференциального уравнения.(цифра)
Дифференциал неопределенного интеграла равен ...
Найти частную производную функции z(x,y) по переменной х
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Значение частной производной df/dy функции f(x,y)=3x2+2y3-7 в точке с координатами (0,1) равно …
Установите соответствие между дифференциальным уравнением и его типом
Дано дифференциальное уравнение y’+2ytgx=0
Укажите последовательность определения условного экстремума функции двух переменных методом множителей Лагранжа
найти точки экстремума (приравнять к 0 и решить систему)
составить функцию Лагранжа ()
определить значение функции в этой точке
Начало формы
Найти частную производной функции z(x,y) по переменной x
Найти частную производную функции z(x,y) по переменной x в точке (0,0)
Укажите правильное значение производной от неопределенного интеграла
Для указанных рядов определите сходимость и ее вид.
Укажите правильное значение интеграла
Укажите правильное значение интеграла
Среди перечисленных ниже выражений укажите правильное для следующего интеграла:
Производная от первообразной для данной функции равна
Радиус сходимости – R степенного ряда c0+c1x+c2x2+… cnxn+… находится из выражения…
Разложение функции y=ex в ряд Маклорена имеет вид …
Разложение функции
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Радиус сходимости
Задание: указать число точек экстремума функции. Ниже указана последовательность действий для нахождения точек.
Укажите геометрический смысл определенного интеграла от функции y=f(x), заданной на отрезке [a,b]?
Разложение функции y=cos(x) в ряд Маклорена имеет вид …
Определите градиент функции f(x,y)=4x+2xy-10
Разложение функции y=ex по степеням (x-2) имеет вид …
Найти частную производную функции z(x,y) по переменной x в точке (0,0)
Среди перечисленных ниже выражений укажите правильное для следующего интеграла
Для указанных рядов определите сходимость и ее вид.
Каков геометрический смысл определенного интеграла для положительной функции y=f(x), заданной на отрезке [a,b]?
Укажите правильное значение интеграла
Укажите отличие понятий определенного и неопределенного интегралов
Дано дифференциальное уравнение:
Найти частную производную функции z(x,y) по переменной x в точке (0,0)
Найти частную производной функции z(x,y) по переменной х
Вычислить значение частной производной функции z(x,y) по переменной x в точке (0,0)
Для указанных последовательностей укажите формулу общего члена
Частная производная первого порядка функции двух переменных по своему геометрическому смыслу представляет
Мы, ни раз, сдавали тесты по данному предмету и уверенно можем сказать: "Сделаем тест на хороший балл". Результаты сдачи, данного предмета, можете посмотреть во вкладке "Результаты"
Если необходима помощь, доверьте выполнения теста нам, так как, мы знакомы с Вашей системой тестирования.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)

- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.

2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:

- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


