-
ВЫ СТУДЕНТ ММУ (Московский Международный Университет)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Математические основы теории управления (1-1) ММУ
О НАС
Меня зовут Сергей, 8 лет я решаю тесты и пишу работы по данному предмету для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
Курсовая работа
НАПИШЕМ КУРСОВУЮ, НА ЛЮБУЮ ТЕМУ ПО ДАННОМУ ПРЕДМЕТУ.
Для уточнения стоимости и заказа работы, напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ.
Мы знакомы с требованиями для курсовых работ по данному предмету.
Выполняем работу полностью (текст, титульны, антиплагиат), при необходимости сами загружаем и контролируем выставление оценки.
Заказав работу у нас, Вам не нужно ни чего делать и дорабатывать.
Контрольная работа
ВЫПОЛНИМ ПРАКТИЧЕСКУЮ (СЕМИНАР) ПО ДАННОМУ ПРЕДМЕТУ.
С 01.09.2019 г. практические работы стали обязательными в ММУ, не выполнив практическую, не получите положительную оценку, даже если сдадите тесты на 5 баллов.
Закажите работу прямо сейчас и получите полностью оформленную работу, мы можем самостоятельно загрузить работу в личный кабинет и проконтролировать выставление оценки.
Для уточнения стоимости и заказа работы, напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ.
Ответы на тесты ММУ
РЕШИМ ТЕСТ ММУ НА ХОРОШУЮ ОЦЕНКУ.
Решаем тесты, для этого вуза, более 5 лет. Знаем все требования и процедуру сдачи. Закажите решение теста по данному предмету и получите хорошую оценку, работаем самостоятельно, не нанимаем сторонних лиц, поэтому конфиденциальность гарантируем.
Напишите нам, по любому каналу связи, размещённому на данной странице, во вкладке КОНТАКТЫ или через ОНЛАЙН ЧАТ. И В КАЧЕСТВЕ ТЕСТА НАШИХ УСЛУГ, ПЕРВЫЙ ТЕСТ СДАДИМ БЕСПЛАТНО (тест сдается бесплатно, если ранее ни чего у нас не заказывали, проверка по логину).
Результаты наших решений, можете посмотреть во вкладке "РЕЗУЛЬТАТЫ".
Тестирование проходит на официальном сайте ММУ в личном кабинете ЭИОС https://elearn.interun.ru.
Оценка выставляется, по лучшему результату.
ВОПРОСЫ ТЕСТА ММУ ПО ДАННОМУ ПРЕДМЕТУ:
Переведите комплексные числа в алгебраическую форму записи \frac{2}{\sqrt{3}} \cdot e^{j\pi/3}
Переведите комплексные числа в алгебраическую форму записи
Вычислите определитель матрицы \large\left(\begin{array}{ccc}9&8&5\\2&3&4\\3&2&1\end{array}\large\right)
Вычислите определитель матрицы
Вычислите модуль комплексного числа (-\sqrt{3}-j)
Вычислите модуль комплексного числа
Запишите комплексное число j в тригонометрической форме
Вычислитьопределителиматриц \large\left(\begin{array}{rrr}9&-8&10\\-2&3&-12\\3&-2&8\end{array}\large\right)
Вычислить определители матрицПолучите частное в алгебраической форме записи \frac{-{\rm 2}+{\rm 5}j}{-{\rm 3}\, -{\rm 4}j}
Получите частное в алгебраической форме записи
Переведите комплексное число e^{j\pi/2} в алгебраическую форму записи
Переведите комплексное число в алгебраическую форму записи
Вычислить определители матриц \large\left(\begin{array}{ccc}7&3&2\\6&1&4\\5&8&9\end{array}\large\right)
Вычислить определители матрицВычислить определители матриц \large\left(\begin{array}{ccc}2&9&8\\7&6&5\\4&3&3\end{array}\large\right)
Вычислить определители матриц
Вычислить определители матриц \large\left(\begin{array}{rrr}9&10&5\\-2&-12&-4\\3&8&-1\end{array}\large\right)
Вычислить определители матриц
Вычислите модуль комплексного числа (-3 + 4j)
Получите разность чисел 3 + 2j и –3 + 2j
Cложите комплексные числа –3 + 5j и 4 – 8j
Перемножьте комплексные числа –3 + j и –3 – j
Найти решение систем уравнений матричным способом \left. \begin{array}{l} {7x+2y+3z=13} \\ {9x+3y+4z=15} \\ {5x+y+3z=14} \end{array}\right\}
Найти решение систем уравнений матричным способомПолучите частное в алгебраической форме записи \frac{-6+21j}{4-14j}
Получите частное в алгебраической форме записиЗапишите комплексное число (\sqrt{3} -j).в тригонометрической форме
Запишите комплексное число . в тригонометрической форме
Cложите комплексные числа 2 + 0j и 7 + 0j
Вычислить определители матриц \large\left(\begin{array}{ccc}3&6&4\\4&5&2\\8&1&9\end{array}\large\right)
Вычислить определители матрицВычислить определитель матрицы \large\left(\begin{array}{ccc}4&6&4\\3&5&2\\1&9&7\end{array}\large\right)
Вычислить определитель матрицыЗапишите комплексные числа в тригонометрической форме (1 + j)
Запишите комплексное число 3j в тригонометрической форме
Определите аргумент комплексного числа (- \sqrt{3} -j)
Определите аргумент комплексного числа
Получите разность чисел 1 + j и 2 – 5j
Запишите комплексные числа в тригонометрической форме (-\frac{1}{2}-j\frac{\sqrt{3} }{2})
Запишите комплексные числа в тригонометрической форме
Определите аргумент комплексного числа (-3 + 4j)
Найти решение систем уравнений матричным способом \left.\begin{array}{l} 9x -8y+5z=10 \\ -2x+3y-4z=-12 \\ 3x -2y -z=8\end{eqnarray}\right\}
Найти решение систем уравнений матричным способомПереведите комплексные числа в алгебраическую форму записи \frac{1}{\sqrt{2}} \cdote^{-j3\pi/4}
Переведите комплексные числа в алгебраическую форму записиОпределите аргумент комплексного числа (2 + 2j)
Найти решение систем уравнений матричным способом \left. \begin{array}{l} {x+y=1} \\ {2x+7y=-3} \end{array}\right\}
Найти решение систем уравнений матричным способомРешите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + х = e–t + 2·1(t)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? + 4х = cos t
Получите изображение следующей функции F(t) = e^{5t} - 1(t)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
5х? + 8x + 4? xdt = 20·1(t)
Получите изображения следующей функции f(t) = 2sin t \cdotcos t - 2t
Укажите оригинал, соответствующий приведенному ниже изображению F\left(s\right)=\frac{14}{\left(s-2\right)^{3} }
Получите изображения следующей функции f(t) = t \cdotsin 2t
Получите изображение следующей функции f(t) = t \cdot e^{-0,5t}
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{1}{\left(s+1\right)^{2} \left(s+3\right)}
Получите изображения следующей функции f(t) = 0,25 \cdot e^{-2t} \cdotsin 4t
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение x" + 8x' + 7x = 2t + 2 \cdot 1(t)
Получите изображения следующей функции f(t) = e^{at} \cdotcos j \cdot t
Получите изображение следующей функции f(t) = g \cdote^{-at} \cdotsingt , где g и aconst
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + 2x + ?xdt = 16? e3tdt
Получите изображения следующей функции f(t) = cos (4t - 6) \cdot e^{-3t}
Определите оригинал, соответствующий приведенному изображению F\left(s\right)=\frac{s^{2} +1}{s\left(s+1\right)\; \left(s+2\right)}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + 3х? + 2x = 4t
ЗапишитеоригиналысоответствующиеприведеннымнижеизображениямF\left(s\right)=\frac{5s+3}{\left(s-1\right)\; \left(s^{2} +2s+5\right)}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение x" + 10x' + 74x = \delta (t)
ЗапишитеоригиналысоответствующиеприведеннымнижеизображениямF\left(s\right)=\frac{3s}{\left(s^{2} +1\right)^{2} }
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение 2х?? + 9х? + 10х? = ?(t – 9)
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{8s+10}{s^{2} -3s-28}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? – 4х? = 4e2t
Получите изображение следующей функции f(t) = t2 \cdotsin \omega t
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{s^{2} }{\left(s^{2} +4\right)\; \left(s^{2} +9\right)}
Укажитеоригинал, соответствующийприведенномуизображению F{\rm (}s{\rm )}=\frac{{\rm (}s^{{\rm 2}} -{\rm 4)}}{s^{{\rm 2}} {\rm(}s^{{\rm 2}} +{\rm 4)}}
Получите изображения следующей функции f(t) = 8j \cdot e^{jt} \cdotsin t
Получите изображения следующей функции f(t) = 6[\delta(t - 3) - sin t]
Укажите оригинал, соответствующий приведенному ниже изображению F\left(s\right)=\frac{1-e^{-3s}}{s}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? + 6х? + 5x = 8e–3t
Вычислить определители матриц \large\left(\begin{array}{ccc}1&2&3\\7&4&5\\8&9&6\end{array}\large\right)
Переведите комплексное число 2\cdot e^{j\pi } в алгебраическую форму записи
Перемножьте комплексные числа 1 – 2j и 3 + 2j
Вычислить определитель матрицы \large\left(\begin{array}{ccc}5&8&9\\4&3&2\\1&2&3\end{array}\large\right)
Запишите комплексное число (-2)в тригонометрической форме
Вычислитеопределительматрицы \large\left(\begin{array}{rrr}9&-8&5\\-2&3&-4\\3&-2&-1\end{array}\large\right)
Запишите комплексное число (2 + 5j) в тригонометрической форме
Запишите комплексные числа в тригонометрической форме (-2 -5j)
Определите аргумент комплексного числа (1 + j)
Запишите комплексное число (-2 + 5j).в тригонометрической форме
Вычислить определители матриц \large\left(\begin{array}{ccc}4&6&3\\3&5&4\\1&9&8\end{array}\large\right)
Переведите комплексное число 2 \cdot e^{-j4\pi/3} в алгебраическую форму записи
Вычислите модуль комплексного числа (1 + j)
Найти решение систем уравнений матричным способом \left.\begin{array}{l} 4x+6y+4z=3 \\ 3x+5y+2z=4 \\ x+7y+7z=8 \end{eqnarray}\right\}
Вычислите модуль комплексного числа (3 + 5j)
Перемножьте комплексные числа 6 – j и –5 + j
Переведите комплексные числа в алгебраическую форму записи 6 \cdot e^{j\pi/6}
Получите частное \frac{7-4j}{3+2j} в алгебраической форме записи,
Вычислитьопределителиматриц \large\left(\begin{array}{ccc}4&3&4\\3&4&2\\1&8&7\end{array}\large\right)
Cложите комплексные числа 0 + 2j и 0 – 5j
Запишите комплексное число (2 - 5j) в тригонометрической форме
Получите разность чисел 2j и –7
ЗапишитеоригиналысоответствующиеприведеннымнижеизображениямF{\rm (}s{\rm )}=\frac{{\rm 3(}s-{\rm 1)}}{s^{{\rm 2}} +4}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение x" + 8x' + 7x = \delta(t-3)
Получите изображение следующей функции ?(t) = 5•e3t•?(t – 7)
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{2}{\left(s-8\right)^{3} }
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
Получите изображения следующей функции f(t) = t \cdotcos 4t
Получите изображение следующей функции f(t) = t \cdot 1(t - a) Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + 6х? + 9x = ?(t)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + х = sin 2t
Получите изображения следующей функции f(t) = e^{2t} \cdotsin (t - 3)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение 2x" + 10x' + 8x = sin3t
Получите изображения следующей функции f(t) = 8 \cdotcos^{2} t
Получите изображения следующей функции F(t) = 0,25t - 0,125sin 2t
Какой из оригиналов соответствует приведенному изображению F\left(s\right)=\frac{s+1}{s^{2} \left(s-1\right)\left(s+2\right)}
Укажите оригинал, соответствующий приведенному изображениюF\left(s\right)=\frac{s+1}{\left(s-1\right)\; \left(s^{2} +2s-3\right)}
Получите изображения следующей функции f(t) = t^2 \cdot e^{7t}
Запишите оригинал, соответствующий приведенному ниже изображению F\left(s\right)=\frac{1}{\left(s^{2} +6s+13\right)\; \left(s^{2} +6s+5\right)}
Определитеоригинал, соответствующийприведенномуизображению F\left(s\right)=\frac{s-\left(s-3\right)\cdot e^{-2s} }{s\left(s-3\right)}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? + х? = cos t
Определите аргумент комплексного числа (3 + 5j)
Определите аргумент комплексного числа (-1 + j \sqrt{3} )
Перемножьте комплексные числа –7 – 4j и 5 + 8j
Переведите комплексные числа в алгебраическую форму записи \frac{\sqrt{2} }{2} \cdot e^{j5\pi/6}
Запишите комплексное число ( -3j) в тригонометрической форме
Вычислите модуль комплексного числа (-1 + j\sqrt{3} )
Вычислитьопределителиматриц \large\left(\begin{array}{rrr}10&-8&5\\-12&3&-4\\8&-2&-1\end{array}\large\right)
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{s+7}{\left(s+7\right)^{2} +9}
Получите изображение следующей функции f(t) = 2 \cdot sin^2(t - 7)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение x"- 9x = 2 \cdot 1(t) - 2t
Вычислитьопределителиматриц \left(\begin{array}{ccc} {1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right)
Получите изображение следующей функции ?(t) = 15?(t – 2)
Получите изображение следующей функции f(t) = t \cdot e^{-0,5t}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
х? + 4х = 2sin 2t
Укажитеоригинал, соответствующийприведенномуизображению F\left(s\right)=\frac{1}{\left(s+1\right)^{3} \left(s+3\right)}
Запишитеоригиналысоответствующиеприведеннымнижеизображениям F\left(s\right)=\frac{3s}{\left(s^{2} +1\right)^{2} }
Получите изображение следующей функции f(t) = 3(t - 2) \cdot e^{5t}
Определитеоригинал, соответствующийприведенномуизображению F\left(s\right)=\frac{s^{2} -16}{\left(s^{2} +16\right)^{2} }
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{1}{\left(s+2\right)^{2} +16}
Переведите комплексные числа в алгебраическую форму записи 2 \cdot e^{j2\pi/3}
Переведите комплексное число -3\cdot e^{-j\pi } в алгебраическую форму записи
Получите разность чисел 3 – 4j и 3 + 4j
Перемножьте комплексные числа –3 + j и –3 + j
Запишите комплексные числа в тригонометрической форме (-1+j\sqrt{3})
Получите изображение следующей функции f(t) = [12t - 24 \cdot 1(t)] \cdot e^{4t}
Определите оригинал, соответствующий приведенному изображению F\left(s\right)=\frac{s^{2} +1}{s\left(s+1\right)\; \left(s+2\right)}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? + х = cos t + sinПолучите изображения следующей функции ?(t) = 13•e–2t•?(t – 5)
Запишите комплексные числа в тригонометрической форме (1-j\cdotsqrt{3})
Переведите комплексные числа в алгебраическую форму записи \frac{2}{\sqrt{3}} \cdot e^{j5\pi/6}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение х? – 3х? + 2x = 4t2
Запишитеоригиналысоответствующиеприведеннымнижеизображениям F\left(s\right)=\frac{s+1}{\left(s-1\right)\; \left(s^{2} +9s+20\right)}
Получите разность чисел –5 + 2j и 3 – 5j
Cложите комплексные числа –2 + 3j и –2 – 3j
Запишите комплексное число (-1 - j) в тригонометрической форме
Запишите оригиналы соответствующие приведенным ниже изображениям F(s)=\frac{5(s-2)}{(s+2)^{2} +9}
Получите изображение следующей функции f(t) = 3t \cdote^{at} , где а – const
Получите изображения следующей функции f(t) = e^{(t - 8)} \cdotsint
Запишитеоригиналысоответствующиеприведеннымнижеизображениям F\left(s\right)=\frac{1}{\left(s+2\right)^{2} \left(s+1\right)}
Запишитеоригиналысоответствующиеприведеннымнижеизображениям F\left(s\right)=\frac{s+5}{\left(s+3\right)^{2} +4} \cdot e^{-2s}
Какой из оригиналов соответствует приведенному изображению F\lef(s\right)=\frac{4s}{\left(s^{2} +4\right)^{2} }
Запишите комплексное число (-\frac{\sqrt{3}}{2}\,+j\cdot\frac{1}{2}) в тригонометрической форме
Запишите комплексное число (-j)в тригонометрической форме
Укажите оригинал, соответствующий приведенному изображению F{\rm (}s{\rm )}=\frac{{\rm (}s^{{\rm 2}} -{\rm 4)}}{s^{{\rm 2}} {\rm (}s^{{\rm 2}} +{\rm 4)}}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение 4х″ + 8х′ + 5x = δ(t)
Запишите оригиналы соответствующие приведенным ниже изображениямОпределите оригинал, соответствующий приведенному изображениюПолучите изображение следующей функции f(t) = (t - 2) \cdot 1(t - 2)
Запишите комплексное число 2 в тригонометрической форме.
Запишите комплексное число 1 в тригонометрической форме
Получите изображения следующей функции f(t) = [12t - 6 \cdot 1(t)] \cdot e^{4t}
Получите изображение следующей функции f(t) = cos (\omega t - a)
Запишите оригиналы соответствующие приведенным ниже изображениямОпределите оригинал, соответствующий приведенному изображению F\left(s\right)=\frac{s-\left(s-Запишите оригиналы соответствующие приведенным ниже изображениям F{\rm (}s{\rmПолучите изображение следующей функции ƒ(t) = 15δ(t – 2)
Получите изображение следующей функции f(t) = 3t \cdot e^{at} , где а - const
Получите изображение следующей функции f(t) = t \cdot 1(t - a)
Получите изображение следующей функции f(t) = [12t - 24 \cdot 1(t)] \cdot e^{4t}
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
Вычислите модуль комплексного числа (-2 + 2j)
Решите операторным методом (на основе преобразования Лапласа) следующее уравнение
Запишите оригинал, соответствующий приведенному ниже изображению F\left(s\right)=\frac{1}{\left(s^{2} +6s+13\right)\; \left(s^{2} +6s+5\right)}
Укажите оригинал, соответствующий приведенному изображению
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{5\left(s-2\right)}{\left(s-2\right)^{2} +9}
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{s+5}{\left(s+3\right)^{2} +4} \cdot e^{-2s}
Определите оригинал, соответствующий приведенному изображению F\left(s\right)=\frac{s^{2} -16}{\left(s^{2} +16\right)^{2} }
Получите изображение следующей функции f(t) = g \cdot e^{-at} \cdot sin gt , где g и a const
Cложите комплексные числа \sqrt{3} -j\, и \, 1- j\sqrt{3}
Получите изображения следующей функции f(t) = t^2 \cdot e^{7t}
Получите изображение следующей функции f(t) = t \cdot e^{-0,5t}
Получите изображения следующей функции f(t) = 2sin t \cdot cos t - 2t
Вычислить определители матриц \left(\begin{array}{ccc} {1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right)
Получите изображение следующей функции f(t) = t2 \cdot sin \omega t
Запишите оригиналы соответствующие приведенным ниже изображениям F(s)=\frac{5(s-2)}{(s+2)^{2} +9}
Получите изображения следующей функции f(t) = 8j \cdot e^{jt} \cdot sin t
Запишите оригиналы соответствующие приведенным ниже изображениям F\left(s\right)=\frac{3s}{\left(s^{2} +1\right)^{2} }
Вычислите определитель матрицы \large\left(\begin{array}{rrr}9&-8&5\\-2&3&-4\\3&-2&-1\end{array}\large\right)
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2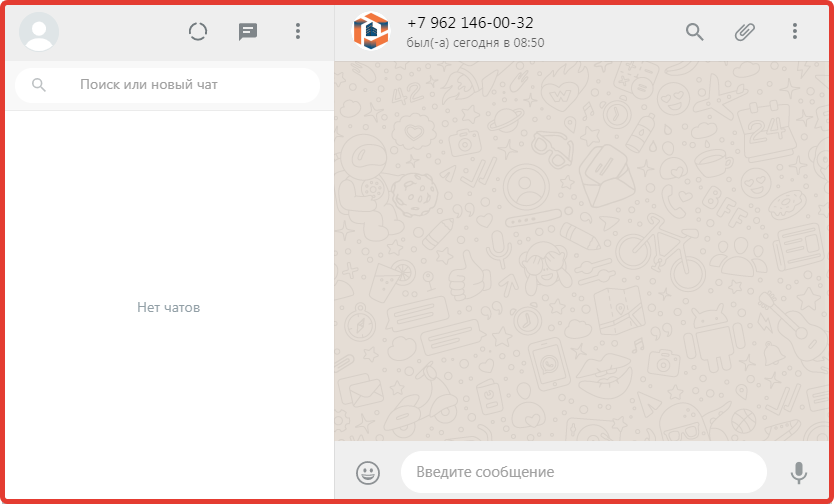
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3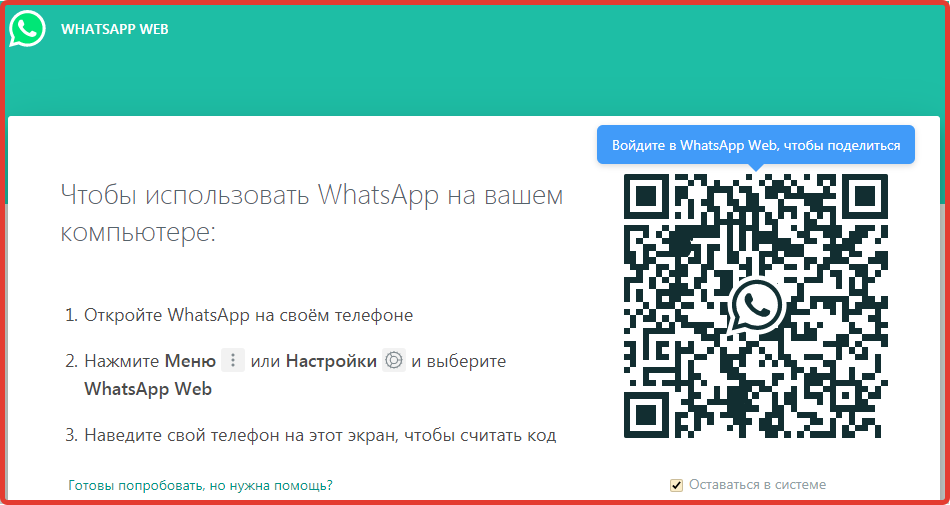
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
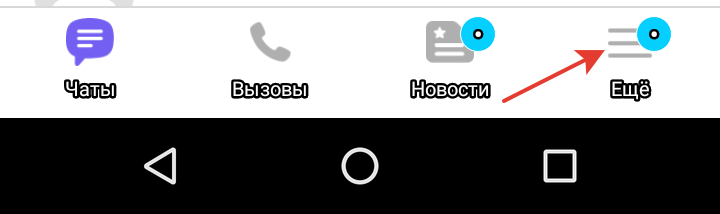
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
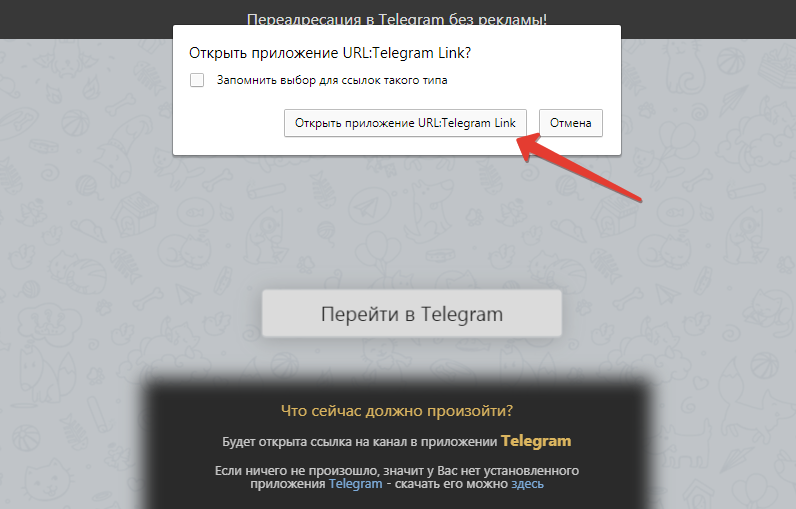
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


