-
ВЫ СТУДЕНТ МИЭП (Международный Институт Экономики и Права)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Линейная алгебра МИЭП
О НАС
Меня зовут Сергей, 10 лет я решаю тесты и пишу работы по данному предмету, для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Высокий процент сдачи тестов.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3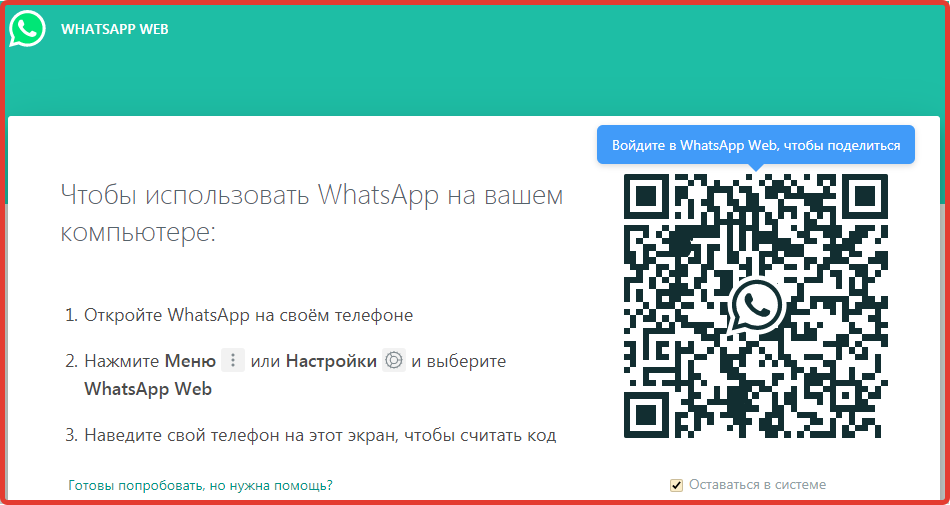
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:
Курсовая работа
По данному предмету, данный вид работы не предусмотрен.
Мы, ни раз, писали КР (курсовые работы) по данному предмету и уверенно можем сказать: "Сделаем по всем требованиям". Вам останется только сдать работу, пишем работу полностью, оформляем, вставляем титульный лист, все работы проверям на антиплагиат, если будут замечания исправляем бесплатно.
Если необходима помощь, доверьте написания КР нам, так как, мы знакомы с требованиями Вашего ВУЗа, работаем профессионально и оперативно.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Ответы на тесты МИЭП
Тестирование проходит на официальном сайте МИЭП http://sdo1.miep.ru и http://sdo.miep.ru Оценка выставляется, по первому положительному результату.
Вопросы для подготовки к тестированию:
-
Начало формы
Конец формы
Начало формы
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если:
Конец формыНачало формыВыяснить, какие из следующих операций можно выполнить:
Конец формыНачало формы
Конец формы
Начало формы
Чему равен ранг единичной матрицы Е?
Конец формыВ результате произведения квадратных матриц получено, что А*В=А и В*А=А. Следовательно, матрица В по отношению к матрице А является:
Начало формы
Конец формы
Начало формы
Найти |D| = ?
Конец формыДля системы из 2-х линейных уравнений подсчитаны определители: D = 0; D(x) = 20; D(y) = 10. Эта система:
Начало формы
Конец формы
Начало формы
Выяснить, какие из следующих операций можно выполнить:
Конец формыВырожденной матрицей называется:
Начало формы
Конец формы
Начало формы
Вычислите определитель матрицы
Конец формыНачало формы
Какая из перечисленных матриц имеет обратную?
Конец формыОбратной, по отношению к единичной матрице Е, является
Определить след единичной матрицы A третьего порядка (trA)?
Начало формы
Определите длину следующего вектора:
Конец формыНачало формы
Конец формы
Начало формы
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если:
Конец формыВ результате умножения 2-х матриц А и В получена единичная матрица E: AB = E. Следовательно, матрица В по отношению к А является:
Начало формы
Чему равен след матрицы А (trA)?
Конец формыНачало формы
Результатом транспонирования единичной матрицы Е является?
Конец формыДана система линейных уравнений у которой число уравнений равно числу неизвестных. При каком условии эта система имеет единственное решение?
Начало формы
Что представляет собой результат умножения С=А*В?
Конец формыНачало формы
Конец формы
Совместная система линейных уравнений имеет бесконечное множество решений, если
Результатом транспонирования единичной матрицы Е является?
Определить след единичной матрицы A третьего порядка (trA)?
Выяснить, какие из следующих операций можно выполнить: (ПТК: тема 1, задание 2)
Выяснить, какие из следующих операций можно выполнить: Даны матриц А=(2 0; 5 1) B=(5 4; 7 2; 2 1)
Какая из перечисленных ниже матриц является единичной?
Дана матрица АНайти |D| = ? |D|=|1 2 7 9; 1 3 7 8; 1 4 7 1; 1 5 7 0|
Вычислите определитель матрицы |D|=|0 1 1; 1 0 1; 1 1 0|
Вычислить значение определителя|D|=|0 1 1; 1 0 1; 1 1 0|
Вычислить следующий определитель: |D|=|0 1 1; 1 0 1; 1 1 0|
Чем отличается минор М43 от алгебраического дополнения А43?
Минор и алгебраическое дополнение элемента матрицы.
(ПТК: тема 3, задание 2)
Чем отличается минор М43 от алгебраического дополнения А43?
Чем отличается минор М48 от алгебраического дополнения А48?
Укажите правильное значение алгебраического дополнения –А12 матрицы А=(1 3; 2 4): а) А12=1; б) А12=2; в) А12=3; г) А12=4; д) А12=-1; е) А12=-2; ж) А12=-3; г) А12=-4;
Алгебраическое дополнение элемента матрицы.
(ПТК: тема 3, задание 2)
Какая из перечисленных матриц имеет обратную?
Чему равен ранг единичной матрицы Е? Е=(1 0 0; 0 1 0; 0 0 1)?
Какой из перечисленных ниже методов решения системы линейных уравнений требует вычисления обратной матрицы? (ПТК: тема 4, задание 1.3)
Дана система линейных уравнений у которой число уравнений равно числу неизвестных.При каком условии эта система имеет единственное решение?
Согласно теореме Кронекера - Капелли, система линейных уравнений совместна тогда и только тогда, когда:
Совместная система линейных уравнений имеет бесконечное множество решений, если
На плоскости заданы три вектора: А, В и С. Вектор С может быть представлен линейной комбинацией векторов А и В:
Конец формыКонец формы
Начало формы
Среди указанных ниже, вектор, ортогональный вектору а=(3; -1) равен
Конец формыКонец формы
Симметрическая матрица квадратичной формы симметрична относительно …
Начало формыКонец формыКонец формы
(ПТК: тема 6, задание 2)
Вектор y =A(x), определяемый посредством линейного оператора А(х), называется…
Начало формы(ПТК: тема 6, задание 1)
Вектор x=
Для указанных ниже матриц А, В, С и D:
Начало формыКонец формы
Начало формы
Конец формы
Даны три вектора: A=(0, 0, 0); B=(0, 1, 0); и С=(1, 0, 0). Определить, могут ли они образовать базис трехмерного евклидова пространства.
С этой целью:
1. Проверьте наличие нулевого вектора. Сформулируйте необходимость наличия нулевого вектора в базисе линейного пространства;
2. Проверьте линейную независимость векторов;
3. Проверьте пьопарную ортогональность векторов;
4. Вычислите норму (величину) каждого вектора;
5. Сделайте вывод, опираясь на полученные результаты.
6. Вывод:
а) заданные вектора образуют ортогональный, ортонормированный базис трехмерного евклидова пространства;
б) заданные вектора не могут быть использованы в качестве базиса евклидова пространства, так как среди них имеется нулевой ветор;
в) заданные вектора могут быть использованы в качестве базиса евклидова пространства поскольку среди них имеется нулевой ветор.
Даны три вектораРанг матрицы
Матрица не имеет обратной при λ равном
Определитель
Определитель
Определитель
Определитель
ОпределительОпределите тип кривой
Каноническое уравнение эллипса с полуосями a = 4 и b = 3,
c центром в начале координат имеет вид
(ПТК: тема 9, задание 1)
Каноническое уравнение эллипса с полуосями
Матрице
Проверить знакоопределенность
Для указанной ниже системы линейных уравнений, выполните следующие действия:
(тема 4 , задание 1 ПТК)
Конец формыПроверить знакоопределенность квадратичной формы.
(ПТК: тема 7, задание 1)
Проверить знакоопределенность квадратичной формы. (ПТК: тема 7, задание 1)
Для указанной ниже матрицы А, выполните следующие действия
(ПТК: тема 3, задание 1) Для указанной ниже квадратичной формы L(x1,x2), выполните следующие действия:
(ПТК: тема 7, задание 1)
Расположите векторы p=(0; 7), q=(3; 4) и l =(6, 0) в порядке убывания их длины.
(ПТК: тема 5, задание 2)
След матрицы А (trA) равен
(ПТК: тема 1, задание 5)
Расположите векторы p=(0; 7), q=(3; 4) и l =(6, 0) в порядке возрастания их длины.
(ПТК: тема 5, задание 2)
Значение определителя равно
(ПТК: тема 2, задание 2)
Определитель матрицы А равен
(ПТК: тема 2, задание 1)
Установите соответствие между видом кривой и ее уравнением
(ПТК: тема 9, задание 1)
Решить уравнение. Значение x равно
(ПТК: тема 2, задание 4)
Укажите правильный порядок действий при вычислении обратной матрицы.
(ПТК: тема 3, задание 2)
Для указанной матрицы А, вычислить определитель матрицы В=А3. Определитель матрицы |В| = |А3| равен
(ПТК: тема 2, задание 2)
Укажите правильный порядок действий при определении знакоопределенности квадратичной формы, используя собственные значения матрицы квадратичной формы
(ПТК: тема 7, задание 1)
Укажите правильный порядок действий при определении знакоопределенности квадратичной формы при использовании критерия Сильвестра.
(ПТК: тема 7, задание 1)
Укажите правильный порядок действий при решении системы алгебраических уравнений методом Крамера
(ПТК: тема 4, задание 2)
(ПТК: тема 1, задание 1)
Для указанных ниже матриц А, В, С и D:
(ПТК: тема 5, задание 2)
Скалярное произведение вектора a=(2;-3;1) и b=(-1;2;-2) равно…
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Вычислите определитель матрицы |D|=|0 1 1; 1 0 1; 1 1 0|
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Для системы из 2-х линейных уравнений с ненулевыми коэффициентами подсчитаны определители: D = 0; D(x) = 0; D(y) = 0. Эта система (ПТК: тема 4, задание 1.2)
(ПТК: тема 5, задание 2)
Значение к
(ПТК: тема 1, задание 1)
Для указанных ниже матриц
(ПТК: тема 2, задание 2)
Дана матрица А=(1 0 0; 2 2 0; 3 3 2). Вычислите определитель матрицы B=A3 и укажите правильный ответ: |B|=|А3|=…
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Вычислить значение определителя |D|=|1 2 7 9; 1 3 7 8; 1 4 7 1; 1 5 7 0|
Результатом транспонирования матрицы - строки является (ПТК: тема 1, задание 3)
Операция транспонирования матрицы НЕ обладает свойством
(ПТК: тема 1, задание 2)
Симметрическая матрица квадратичной формы симметрична относительно (ПТК: тема 7, задание 2)
След матрицы А (trA) равен
(ПТК: тема 1, задание 5)
Чему равен след матрицы А (trA)?
Метод обратной матрицы используется для (ПТК: тема 4 , задание 5)
Дана система линейных уравнений у которой число уравнений равно числу переменных. Эта система имеет единственное решение при условии, что
(ПТК: тема 4, задание 1.1)
Метод Гаусса используется для (ПТК: тема 4, задание 5)
Значение определителя равно
(ПТК: тема 2, задание 2)
След единичной матрицы третьего порядка равен
(ПТК: тема 1, задание 5)
Расставить определители в порядке убывания их величины.
(ПТК: тема 2, задание 1)
Расставить определители в порядке возрастания их величины.
(ПТК: тема 2, задание 1)
Значение определителя равно
(ПТК: тема 2, задание 2)
Для указанной ниже квадратичной формы L(x1, x2), выполните следующие действия:
(ПТК: тема 7, задание 2)
Для квадратичной формы
Значение λ, при котором матрица А не имеет обратной, равно
(ПТК: тема 3, задание 1)
Выяснить, какие из следующих операций можно выполнить: (ПТК: тема 1, задание 2)
Выяснить, какие из следующих операций можно выполнить: дан матрицы А=(2 0; 5 1) B=(5 4; 7 2; 2 1)
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если: (ПТК: тема 4, задание 1)
(ПТК: тема 1, задание 3)
для указанных ниже матриц А,
Правило Крамера позволяет
(ПТК: тема 4, задание 1)
След единичной матрицы А (trA) третьего порядка равен
(ПТК: тема 1, задание 5)
В результате умножения 2-х матриц А и В получена единичная матрица E: AB = E. Следовательно, матрица В по отношению к А является: (ПТК: тема 4, задание 1, 2)
(ПТК: тема 2, задание 1)
Вычислите определитель матрицы А=(1 0 0; 2 2 0; 3 3 3) и укажите правильный ответ
Для системы из 2-х линейных уравнений подсчитаны определители: D = 0; D(x) = 20; D(y) = 10. Эта система (ПТК: тема 4, задание 1.1)
Выяснить, какие из следующих операций можно выполнить: (ПТК: тема 1, задание 1)
Выяснить, какие из следующих операций можно выполнить:
Даны матрицы А=(2 0; 5 1) B=(5 4; 7 2; 2 1)
(ПТК: тема 2, задание 2)
(ПТК: тема 7, задание 1 )
Симметрическая матрица
Совместная система линейных уравнений имеет единственное решение, если: (ПТК: тема 4, задание 1)
(ПТК: тема 6, задание 1)
Характеристический многочлен матрицы А линейного оператора А определяется по средством выражения…
В результате произведения квадратных матриц получено, что А*В=А и В*А=А. Следовательно, матрица В по отношению к матрице А является: (ПТК: тема 1, задание 2)
(ПТК: тема 1, задание 4)
Какая из перечисленных ниже матриц является единичной?
(ПТК: тема 5, задание 2)
Скалярный квадрат вектора а=(-1; 2; -2) равен…
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если: (ПТК: тема 4, задание 1)
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если: А=(1 0; -2 1)
(ПТК: тема 5, задание 2)
Среди матриц В, С и D, найдите матрицу, обратную матрице А, если: (ПТК: тема 4, задание 1)
Совокупность базисных векторов n-мерного пространства (ПТК: тема 5, задание 5)
Определитель нулевой матрицы третьего порядка равен
(ПТК: тема 2, задание 2)
(ПТК: тема 6, задание 1)
Линейный оператор
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Даны три вектора: a=(0, 0, 1); b=(0, 1, 0); и c=(1, 0, 0). Определить, могут ли они образовать базис трехмерного евклидова пространства. С этой целью:
(ПТК: тема 5, задание 5)
Для указанной ниже матрицы А, выполните следующие действия
(тема 3, задание 1 ПТК)
Для матрицы4
Операция умножения матриц.
(ПТК: тема 1, задание 4)
Даны две матрицы: матрица-строка А=(a11 a12 … a1n) и матрица-столбец B=(b11 b21 … bn1), где n>1. Можно ли перемножить эти две матрицы?
(ПТК: тема 5, задание 2)
Модуль вектора а=(-4; 3; 0) равен …
Начало формыМинор элемента матрицы.
(ПТК: тема 3, задание 2)
Укажите правильное значение минора – М22 матрицы А=(1 3; 2 4) а) М22=1; б) М22=2; в) М22=3; г) М22=4;
Умножение матриц.
(ПТК: тема 1, задание 3)
Даны две матрицы: матрица-строка А=(a11 a12 … a1n) и матрица-столбец B=(b11 b21 … bn1), где n>1. Что представляет собой результат умножения C=A*B?
Ранг матрицы А равен
(ПТК: тема 4, задание 5)
Чему равен ранг матрицы А? А=(5 5 5; 5 5 5; 5 5 5)?
(ПТК: тема 1, задание 3)
Что представляет собой результат умножения С=А*В? Даны две матрицы: матрица-столбец А=(a11 a21 … an1) и матрица-строка B=(b11 b12 … bn1), где n>1.
(ПТК: тема 7, задание 2)
Конец формыСимметрическая матрица квадратичной формы
Начало формыОпределитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Найти |D| = ? |D|=|1 0 0 0; 1564 -2 0 0; 245 1267 3 0; 45 936 568 -1|
Определите длину следующего вектора: (ПТК: тема 5, задание 2)
Вырожденной матрицей называется: (ПТК: тема 3, задание 1)
Согласно теореме Кронекера-Капелли, система линейных уравнений совместна тогда и только тогда, когда: (ПТК: тема 4, задание 1)
(ПТК: тема 6, задание 2)
Конец формыСобственные значения
Начало формыОбратной, по отношению к единичной матрице Е, является (ПТК: тема 4, задание 1)
Укажите последовательность прямых на рисунке в порядке возрастания их угловых коэффициентов.
(ПТК: тема 7, задание 1)
Установите соответствие между способом задания прямой и ее уравнением
(ПТК: тема 10, задание 1)
Даны три вектора: а=(0, 0, 0); b=(0, 1, 0); и c=(1, 0, 0). Определить, могут ли они образовать базис трехмерного евклидова пространства. С этой целью:
(ПТК: тема 5, задание 5)
Определитель единичной матрицы третьего порядка равен
(ПТК: тема 2, задание 2)
Укажите последовательность прямых на рисунке в порядке убывания их угловых коэффициентов.
(ПТК: тема 7, задание 1)
Установите соответствие матрицей и ее типом
(ПТК: тема 1, задание 1)
Определитель матрицы |D| равен
(ПТК: тема 2, задание 2)
Для матрицыРанг единичной матрицы Е равен
(ПТК: тема 4, задание 5)
Результатом транспонирования единичной матрицы Е является (ПТК: тема 1, задание 2)
Установите соответствие матрицей и ее типом
(ПТК: тема 1, задание 1)
Мы, ни раз, сдавали тесты по данному предмету и уверенно можем сказать: "Сделаем тест на хороший балл". Результаты сдачи, данного предмета, можете посмотреть во вкладке "Результаты"
Если необходима помощь, доверьте выполнения теста нам, так как, мы знакомы с Вашей системой тестирования.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)

- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.

2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:

- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


