-
ВЫ СТУДЕНТ МИЭП (Международный Институт Экономики и Права)?
ОБУЧАЕТЕСЬ ДИСТАНЦИОННО?
НЕ ПОЛУЧАЕТСЯ ВЫПОЛНИТЬ УЧЕБНОЕ ЗАДАНИЕ?
НАПИШИТЕ НАМ И МЫ ВЫПОЛНИМ ЛЮБОЕ ВАШЕ ЗАДАНИЕ
Если вы учитесь в другом ВУЗе, перейдите по ссылке и выберите свой ВУЗ: СПИСОК ВУЗОВ
Эконометрика МИЭП
О НАС
Меня зовут Сергей, 10 лет я решаю тесты и пишу работы по данному предмету, для Вашего ВУЗа.
Результаты моих работ, можете посмотреть во вкладке «Результаты»
Стоимость выполнения этого предмета, Вы можете узнать, написав мне по любому контакту, во вкладке «Контакты».
- Работы выполняю самостоятельно.
- Высокий процент сдачи тестов.
- Специализируюсь на Вашем ВУЗЕ и знаю все нюансы решения данного предмета.
- Множество каналов связи, для оперативного и удобного общения.
- Полная анонимность, Ваши данные не передаю посторонним лицам.
- При первом обращении, один тест сдаю БЕСПЛАТНО.
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2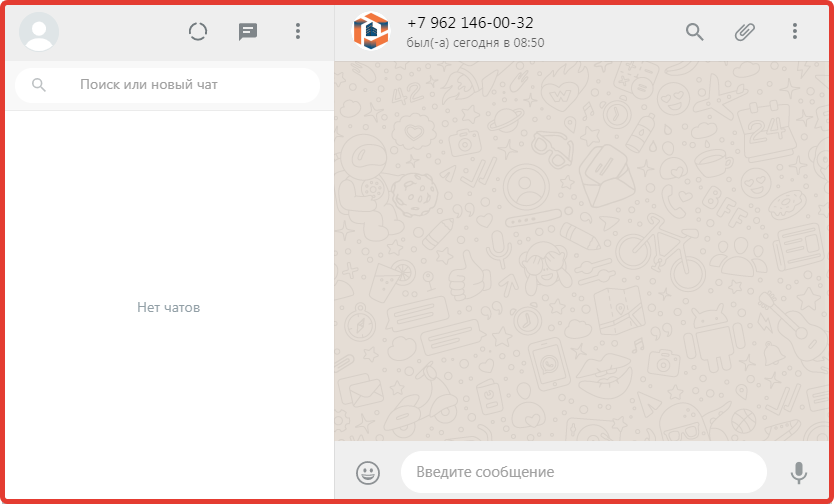
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3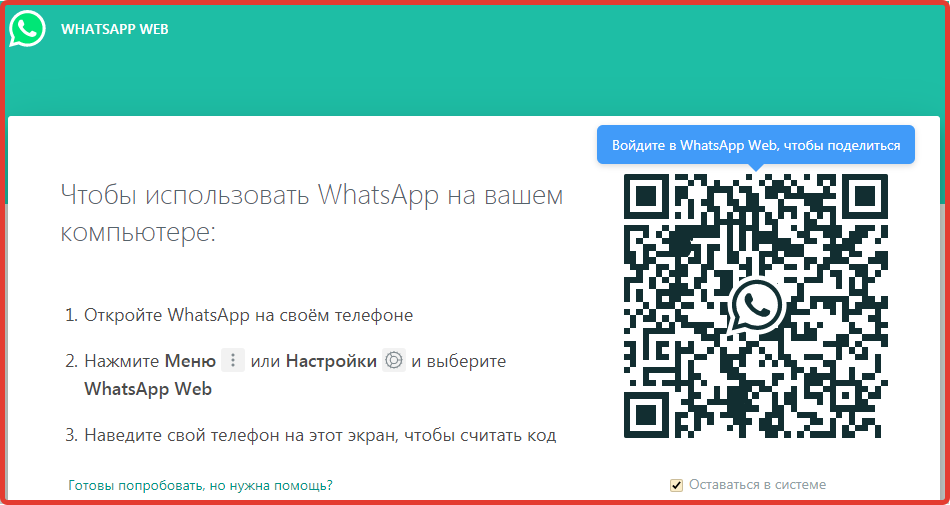
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)
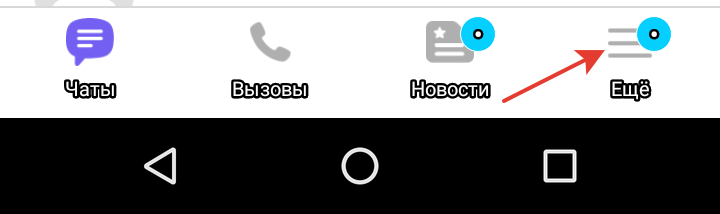
- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
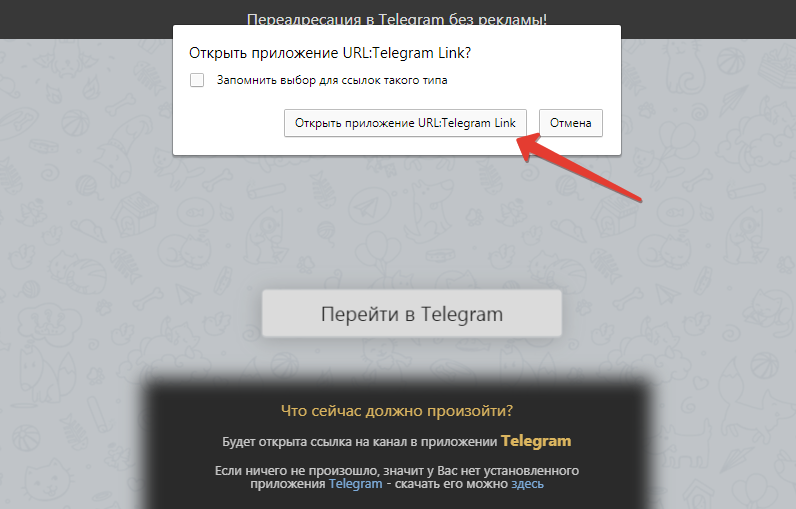
2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:
- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:
Курсовая работа
По данному предмету, данный вид работы не предусмотрен.
Мы, ни раз, писали КР (курсовые работы) по данному предмету и уверенно можем сказать: "Сделаем по всем требованиям". Вам останется только сдать работу, пишем работу полностью, оформляем, вставляем титульный лист, все работы проверям на антиплагиат, если будут замечания исправляем бесплатно.
Если необходима помощь, доверьте написания КР нам, так как, мы знакомы с требованиями Вашего ВУЗа, работаем профессионально и оперативно.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Ответы на тесты МИЭП
Тестирование проходит на официальном сайте МИЭП http://sdo1.miep.ru и http://sdo.miep.ru Оценка выставляется, по первому положительному результату.
Вопросы для подготовки к тестированию:
-
Установите соответствие между критерием и целью его применения:
Для оценки значимости коэффициента корреляции используют критерий (Вес: 1)
Найдите предположение, не являющееся предпосылкой классической модели
Если амплитуда сезонных колебаний на графике временного ряда постоянна, строят ________ модель, в которой значения сезонной компоненты предполагают постоянными для различных циклов
Критерий Дарбина-Уотсона применяется для (ПТК: задание 3, тема 7)
К числовым характеристикам рассеивания (разброса) случайной величины относится (ПТК: задание 2, тема 7)
Коэффициент уравнения регрессии показывает
Величина коэффициента регрессии показывает
На практике гетероскедастичность имеет место, если есть основания считать, что
При гетероскедастичности остатков регрессии применяют ______ метод наименьших квадратов
Какое значение может принимать коэффициент детерминации:
Для точно идентифицированных уравнений двухшаговый метод наименьших квадратов
Корреляционная функция временного ряда – это (ПТК: задание 1, тема 8)
Методы оценивания коэффициентов структурной модели (ПТК: задание 3, тема 9)
Предопределенные переменные включают в себя:
Суть коэффициента детерминации состоит в следующем:
Мультипликативной моделью временного ряда называется модель, в которой все
Существование достаточно тесной линейной связи между некоторыми факторами называется ________
Долю дисперсии зависимой переменной, обусловленную вариацией объясняющей переменной в построенной регрессии, характеризует коэффициент _______
Установите этапы процедуры двухшагового метода наименьших квадратов в верном порядке
Идентификация модели – это:
Системами эконометрических уравнений являются системы
Уровень временного ряда может содержать
Установите соответствие между видом структурной модели и используемым методом наименьших квадратов для определения параметров модели:
Для уравнения регрессии y=a+bx+e метод наименьших квадратов используется при оценивании параметров
При изучении зависимости
Методами выравнивания уровней временного ряда может служить (ПТК: задание 2, тема 7)
Под временным рядом (динамическим рядом) понимается последовательность наблюдений некоторого признака Y, значения которого
Для уравнения регрессии y=a+bx+e метод наименьших квадратов используется при оценивании параметровОбобщенный метод наименьших квадратов не может
применяться для оценки параметров линейных регрессионных
моделей в случае, если ...
Для регрессионной модели несмещенность оценки параметра
означает, что математическое ожидание остатков равно ...
При методе наименьших квадратов параметры уравнения парной
линейной регрессии y = a + b • x + ε определяются из условия ______ остатков ε.
При выполнении предпосылок метода наименьших квадратов
(МНК) оценки параметров регрессионной модели, рассчитанные с
помощью МНК, обладают свойствами ...
Известно, что коэффициент автокорреляции остатков первого
порядка равен -0,3. Также даны критические значения статистики
Дарбина - Уотсона для заданного количества параметров при
неизвестном и количестве наблюдений dL = 0,82, dU = 1,32. По
данным характеристикам можно сделать вывод о том, что ...
Использование линейного уравнения регрессии для описания
нелинейной зависимости показателей является ошибкой _______ эконометрической модели.
Нелинейным по объясняющим переменным, но линейным по
параметрам уравнением регрессии является ...
При идентификации модели множественной регрессии
у = а + b1 · x1 + b2 · x2 + bз · x3 + b4 · x4 + ε количество
оцениваемых параметров равно ...
При идентификации модели множественной регрессии
у = а + b1 · x1 + b2 · x2 + bз · x3 + b4 · x4 + ε количество
оцениваемых параметров равно ...
В модели вида y = a + b1x1 + b2x2 + b3x3 + ε количество
объясняющих переменных равно ...
В эконометрической модели линейного уравнения множественной
регрессии y = a + b1 x1 + b2 x2 + ... + bj xj + ... + bk xk + ε величина
параметра a характеризует среднее по совокупности значение
зависимой переменной, при значениях ___, равных 0.
В эконометрической модели линейного уравнения множественной
регрессии y = a + b1 x1 + b2 x2 + ... + bj xj + ... + bk xk + ε величина
параметра a характеризует среднее по совокупности значение
зависимой переменной, при значениях ___, равных 0.
Примерами фиктивных переменных в эконометрической модели
зависимости стоимости 1 м2 жилья не являются ...
Коэффициент корреляции Rху парной линейной регрессии
у = а + b • х + ε нельзя рассчитать по формуле ...
При линеаризации нелинейных регрессионных моделей как один
из видов преобразований используется логарифмирование
уравнения. Указанным способом может быть линеаризовано
уравнение ...
Для линеаризации нелинейной функции y=a*xb*e
Начало формыРегрессионная модель вида у = а + b · x1 + с · (х2)2 + ε является
нелинейной относительно ...
Регрессионная модель вида у = а + b · x1 + с · (х2)2 + ε является
нелинейной относительно ...
Для регрессионной модели y = f(x) + ε , где f(x) — нелинейная
функция, ỹ = f(х) - рассчитанное по модели значение
переменной У, получено значение индекса корреляции R = 0,64.
Моделью объяснена часть дисперсии переменной У, равная ...
Для регрессионной модели y = f(x) + ε , где f(x) — нелинейная
функция, ỹ = f(х) - рассчитанное по модели значение
переменной У, получено значение индекса корреляции R = 0,64.
Моделью объяснена часть дисперсии переменной У, равная ...
Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
Временной ряд - это совокупность значений экономического
показателя за несколько ______ моментов (периодов) времени.
Изображенный на рисунке временной ряд содержит следующие
компоненты:
Совокупность значений экономического показателя за несколько
последовательных моментов (периодов) времени называется ...
Процесс «белый шум» является ______ временным рядом.
Для стационарного временного ряда y1, y2, ...yt, ..., yn типа
«белый шум» математическое ожидание Е(уt) равно ...
Известно, что временной ряд Y характеризуется устойчивой
тенденцией, то есть его среднее значение меняется. Значит, ряд Y.
скорее всего, является ...
Изображенный на рисунке временной ряд содержит случайную ...
Известно, что общая сумма квадратов отклонений
∑(y - ȳ)= 150, а остаточная сумма квадратов отклонений,
∑(y - ŷx)2 = 30. Тогда значение коэффициента детерминации
равно ...
Для совокупности из n единиц наблюдений построена модель
линейного уравнения множественной регрессии с количеством
параметров при независимых переменных, равным k. Тогда при
расчете остаточной дисперсии на одну степень свободы величину
дисперсии относят к значению ...
Проверка статистически значимого отличия от нуля оценок коэффициентов
Для совокупности из n единиц наблюдений рассчитывают общую
дисперсию на одну степень свободы, при этом величину
дисперсии относят к значению ...
При оценке статистической значимости построенной
эконометрической модели выдвигают _______ гипотезы.
Самым коротким интервалом изменения коэффициента
корреляции для уравнения парной линейной регрессии
у = 2 - 3 ∙ х + ε является ...
В эконометрической модели уравнения регрессии величина
отклонения фактического значения зависимой переменной от
расчетного значения характеризует ...
Для оценки параметров регрессионной модели с
гетероскедастичными остатками используется ______ метод
наименьших квадратов.
Для оценки параметров эконометрической модели линейного уравнения регрессии вида используется метод наименьших квадратов (МНК). В системе нормальных уравнений (МНК) неизвестными величинами являются …
Самым коротким интервалом изменения показателя
множественной корреляции для уравнения множественной
линейной регрессии y = a + b1 ∙ x1 + b2 ∙ x2 + ε, если известны
парные коэффициенты корреляции ryx1 = 0,7,
ryx2 = 0,6, является интервал ...
Если параметр эконометрической модели не является
статистически значимым, то отвергается статистическая гипотеза
о том, что его значение ...
Если параметр эконометрической модели является статистически
значимым, то его значение признается ...
Система независимых эконометрических уравнений может быть
идентифицирована с помощью обычного метода наименьших
квадратов. Определите последовательность этапов алгоритма
оценки параметров для такой модели.
Модель равенства спроса и предложения, где предложение q1 и
спрос q2 являются линейными функциями цены p, состоит из
уравнений ...
Гиперболической моделью не является регрессионная модель ...
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации . Следовательно, доля остаточной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
По 20 регионам страны изучалась зависимость уровня
безработицы y(%) от индекса потребительских цен х(% к предыдущему году) и построено уравнение в логарифмах
исходных показателей: ln y = 0,76 + 0,4 ln · х. Коэффициент
корреляции между логарифмами исходных показателей составил
rln x ln y = 0,8. Коэффициент детерминации для модели в
исходных показателях равен ...
2Нелинейное уравнение парной регрессии вида является _____ моделью.
Нелинейное уравнение парной регрессии вида
у = а + b/x + ε является ______ моделью.
X
Не является полиномом регрессионная модель ...
В эконометрической модели линейного уравнения регрессии
y = a + b1x1 + b2x2 + ... + bjxj + ... + bкхк + ε параметром(-ами)
является(-ются) ...
Если зависимость объема спроса от цены характеризуется
постоянной эластичностью, то моделирование целесообразно
проводить на основе ...
Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3)– независимые переменные):
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
Данная таблица значений автокорреляционной функции соответствует структуре временного ряда …
Для временного ряда известны характеристики: μt - среднее и σt2 - дисперсия. Если временной ряд является стационарным, то ...
Для временного ряда известны характеристики: μt - среднее и σt2 - дисперсия. Если временной ряд является стационарным, то ...
Автокорреляционной функцией временного ряда называется
последовательность коэффициентов автокорреляции ...
Рассмотрим стационарный временной ряд y1, y2, ... yt, ..., yn, для
которого математическое ожидание Е(yt) = 0 (где t = 1, ..., n). Тогда данный стационарный ряд является реализацией процесса
«_____ шум».
Нелинейное уравнение регрессии видау = а + b1x + Ь2x2 + b3x3 + ε является _____ моделью _______
регрессии.
Нелинейным уравнением множественной регрессии является ...
Если для среднеквадратической ошибки параметра и значения оценки этого параметра линейной эконометрической модели выполняется соотношение , то это свидетельствует о статистической ______ параметра.
Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина коэффициента детерминации рассчитывается по формуле …
Для регрессионной модели известны следующие величины дисперсий:
гдеy – значение зависимой переменной по исходным данным; – значение зависимой переменной, вычисленное по регрессионной модели; – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
Для совокупности из n единиц наблюдений построена модель
линейного уравнения множественной регрессии с количеством
параметров при независимых переменных, равным k. Тогда при расчете объясненной дисперсии на одну степень свободы
величину дисперсии относят к значению ...
Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
Количество пар коллинеарных независимых переменных в данной модели равно …
При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать ...
F-статистика рассчитывается как отношение _____ дисперсии к
_____ дисперсии, рассчитанных на одну степень свободы.
Для системы одновременных уравнений , где – процентная ставка, – реальный ВВП, – объем денежной массы, – внутренние инвестиции, – реальные государственные расходы, эндогенными являются переменные …
Система эконометрических уравнений включает совокупность _____ переменных.
Для построения эконометрической модели линейного уравнения регрессии используется таблица статистических данных.
При помощи метода наименьших квадратов (МНК) рассчитываются оценки параметров модели вида . Для выборочного i-го наблюдения модель имеет вид наименьших квадратов минимизируется сумма квадратов …
Для регрессионной модели состоятельность оценки параметра
означает, что при увеличении выборки значение оценки
параметра стремиться к ...
Исходная регрессионная модель имеет вид . Преобразование переменных вида используется в том случае, если ________ и оценка параметров проводится с помощью ________ метода наименьших квадратов.
Для аддитивной модели временного ряда Y = Т + S + Е лаг
модели равен 4 и известны значения трех скорректированных
сезонных компонент: S1 = 2, S2 = -1, S3 = -2. S4 равна ...
Уровень временного ряда (yt) формируется под воздействием
различных факторов - компонент: Т (тенденция), S (циклические
и/или сезонные колебания), Е (случайные факторы). Для
мультипликативной модели временного ряда, содержащего
периодические колебания в 4 момента, получены значения
сезонных компонент: S1 =2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256.
Известны значения компонент: Т5 = 20,6 и Е5 = 0,4. Рассчитайте
значение уровня временного ряда y5.
Дана таблица исходных данных для построения эконометрической регрессионной модели:
не являются Для мультипликативной модели временного ряда Y = T ∙ S ∙ E сумма скорректированных сезонных компонент равна ...
Данная таблица значений автокорреляционной функции соответствует структуре временного ряда ...
Начало формыКонец формы
Метод наименьших квадратов (МНК) может применяться для
оценки параметров исходной регрессионной модели в ______ форме.
Для линеаризации нелинейной функции y = 1 / (a + b ∙ x + ε) может быть применен метод ______ и замены переменных.
По результатам проведения исследования торговых точек было
построено уравнение нелинейной регрессии у = 10·х-0,8, где у - спрос на продукцию, ед.; х - цена продукции, руб. Если
фактическое значение t-критерия Стьюдента составляет -2,05, а
критические значения для данного количества степеней свободы
равны tкр(α = 0,1) = 1,74, tкp(α = 0,05) = 2,11,
tкр(α =0,01) = 2,89, то ...
Модель равенства спроса и предложения, в которой предложение
q1 является линейной функцией цены p, а спрос q2 является
линейной функцией цены р и дохода у, состоит из уравнений ...
Необходимость использования систем эконометрических
уравнений вызвана ...
Для эконометрической модели вида показателем тесноты связи между переменными y и x является парный коэффициент линейной …
Одной из предпосылок метода наименьших квадратов является то.
что в остатках регрессионной модели автокорреляция должна ...
Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
Для линеаризации нелинейной функции у = а ∙ хb ∙ ε может быть
применен метод ...
Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
Для регрессионной модели видаВ эконометрической модели линейного уравнения регрессии y = a + b1x1 + b2x2 + ... + bjxj + ... + bкхк + ? коэффициентом
регрессии, характеризующим среднее изменение зависимой
переменной при изменении независимой переменной на 1
единицу измерения, является ...
Уровень временного ряда (yt) формируется под воздействием
различных факторов - компонент: Т (тенденция), S (циклические
и/или сезонные колебания), Е (случайные факторы).
Мультипликативную модель временного ряда не формируют следующие значения компонент уровня временного ряда ...
Для обнаружения автокорреляции в остатках используется ...
Значение коэффициента автокорреляции первого порядка
характеризует ...
В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,и близок к единице. Это означает, что факторы ,и…
Ошибкой спецификации эконометрической модели уравнения
регрессии является ...
Среди предложенных нелинейных зависимостей нелинейной
существенно (внутренне нелинейной) является ...
В эконометрике фиктивной переменной принято считать ...
В стационарном временном ряде трендовая компонента (ПТК: задание 3, тема 7)
(более одного правильного ответа)
Существование достаточно тесной линейной связи между некоторыми факторами называется ________. (указать в именительном падеже) (ПТК: задание 1,4 тема 2)
Для устранения или уменьшения мультиколлинеарности применяется метод (ПТК: задание 1-4, тема 6)
(более одного правильного ответа)
Укажите этапы процедуры двухшагового метода наименьших квадратов в верном порядке: (ПТК: задание 1,2 тема 4,10)
Соотнесите понятие и определения: (ПТК: задание 1, тема 4,10)
Выбор мультипликативной модели временного ряда осуществляется, если анализ структуры сезонных колебаний показывает, что амплитуда сезонных колебаний (ПТК: задание 1-5, тема 7)
(более одного правильного ответа)
Явление коинтеграции присутствует в случае, если (ПТК: задание 2, тема 7)
(более одного правильного ответа)
Изучение связи между уровнями связных временных рядов проводят с помощью методов коррелирования (ПТК: задание 3, тема 7)
(более одного правильного ответа)
Для получения качественных оценок параметров системы одновременных уравнений используют (ПТК: задание 2, тема 11)
(более одного правильного ответа)
Долю дисперсии зависимой переменной, обусловленную вариацией объясняющей переменной в построенной регрессии, характеризует коэффициент _______. (указать в правильном падеже, отвечая на вопрос «чего?»)
Количество структурных и приведенных коэффициентов одинаково в модели (ПТК: задание 2, тема 9)
Переменные, задаваемые «извне», автономно от модели, называются (ПТК: задание 1, тема 9)
С увеличением числа наблюдений дисперсии МНК-оценок неизвестных параметров в модели регрессии (ПТК: задание 1, тема 5)
Оценки параметров регрессии (свойства оценок МНК) не должны быть (ПТК: задание 3, тема 4)
Аддитивная модель временного ряда имеет вид, если (ПТК: задание 2, тема 7)
Регрессионный анализ заключается в определении (ПТК: задание 4, тема 3)
Для оценки значимости коэффициента корреляции используют критерий (ПТК: задание 4, тема 2)
Определяет среднее изменение результативного признака при изменении факторного признака на 1% коэффициент (ПТК: задание 4, тема 5)
Под временным рядом (динамическим рядом) понимается последовательность наблюдений некоторого признака Y, значения которого (ПТК: задание 1, тема 7)
Гомоскедастичность подразумевает, что ошибки в модели удовлетворяют условию (ПТК: задание 7, тема 1)
Суть метода наименьших квадратов состоит в минимизации суммы (ПТК: задание 1, тема 4)
Коррелирование отклонений от выровненных уровней тренда проводят для (ПТК: задание 5, тема 8)
Связь между признаками Y и Х можно считать тесной (сильной), если значение линейного коэффициента корреляции (ПТК: задание 4, тема 2)
Модель сверхидентифицируема, если число (ПТК: задание 1, тема 11)
На практике гетероскедастичность имеет место, если есть основания считать, что (ПТК: задания темы 7)
Модель идентифицируема, если число (ПТК: задание 1, тема 11)
Величина коэффициента регрессии показывает (ПТК: задание 4, тема 2)
Система уравнений Юла-Уолкера служит для (ПТК: задание 5, тема 7)
Рассчитана матрица парных коэффициентов корреляций (см. рисунок)
Она показывает сильное влияние факторного признака _1__ на результативную переменную__2__ и слабое влияние факторов ___3___. Матрица межфакторных корреляций (матрица парных коэффициентов корреляций без учета __4__ столбца и _5__ строки) характеризуется ___6___ (мультиколлинеарностью, автокорреляцией, гомоскедастичностью).
(ПТК: задание 4, тема 10)
(факторы и паметры вводить с английской раскладки, строчными буквами; индекс вводить просто цифрой, без пробела. Пример: х5; пропущенные слова вводить, соблюдая число, род и падеж по построению фразы).
Построена регрессионная модель в стандартизованном виде (см. рисунок) ост в трен
Параметры такой модели называются ___1__ (дельта, ветта)- коэффициентами. Они позволяют ____2____ (ранжировать, классифицировать) факторные признаки по силе влияния на результат. Фактор __3___ наиболее сильно влияет на результативный фактор, а фактор __4__ может быть исключен из рассмотрения. (ПТК: задание 4, тема 6)
(факторы вводить с английской раскладки, строчными буквами; индекс вводить просто цифрой, без пробела. Пример: х5)Стандартное нормальное распределение имеет параметры (ПТК: задание 1, тема 3)
Если структурные коэффициенты модели выражены через приведенные коэффициенты и имеют более одного числового значения, то такая модель (ПТК: задание 4, тема 10)
Критерий Бартлета предназначен для (ПТК: задание 5, тема 4)
Оценки параметров идентифицируемой системы экономических уравнений могут быть найдены с помощью ___________ МНК. (ПТК: задание 1, тема 10)
Для точно идентифицированных уравнений двухшаговый метод наименьших квадратов дает оценки (ПТК: задание 5, тема 4)
Уравнение тренда представляет собой Y=32,5 – 4,6t. В среднем за год в исследуемом периоде признак изменяется на (ПТК: задание 5, тема 8)
Наличие аномальных наблюдений (выбросов) приводит к (ПТК: задание 5, тема 4)
Метод Гаусса-Ньютона применяется для (ПТК: задание 3, тема 5)
Необходимым условием идентифицируемости системы взаимозависимых
регрессионных уравнений является число априорных ограничений должно быть (ПТК: задание 3, тема 11)
Экзогенные переменные модели характеризуются тем, что они (ПТК: задание 1, тема 9)
Уровень временного ряда может содержать (ПТК: задание 3, тема 7)
Для оценки значимости уравнения регрессии используют критерий (ПТК: задание 1-5, тема 7)
Коэффициент уравнения регрессии показывает (ПТК: задание 3, тема 3)
Под частной корреляцией понимается (ПТК: задание 4, тема 6)
При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной у не может определяться на основании ____________ (линеаризованного, нелинейного, линейного) уравнения регрессии. (ПТК: задание 1-5, тема 4)
При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной у не может определяться на основании ____________ (линеаризованного, нелинейного, линейного) уравнения регрессии. (ПТК: задание 1-5, тема 4)
Установите соответствие между критерием и целью его применения: (ПТК: задание 1,2 тема 4,10)
Согласно содержанию регрессии, наблюдаемая величина зависимой (объясняемой)
переменной складывается из теоретического значения зависимой переменной, найденного из уравнения регрессии и … (ПТК: задание 2, тема 3)
Структурные коэффициенты модели можно оценить тогда, когда модель (ПТК: задание 1, тема 11)
Тренд является частью компоненты временного ряда (ВР) (ПТК: задание 2, тема 8)
Предметом эконометрики является (ПТК: задание 1, тема 1)
Для уравнения регрессии y=a+bx+e метод наименьших квадратов используется при оценивании параметров (ПТК: задание 1, тема 4)
Критические значения критерия Стьюдента определяются по (ПТК: задание 4, тема 5)
Аналогом понятия «эндогенная переменная» является (ПТК: задание 1, тема 9)
Суть коэффициента детерминации состоит в следующем (ПТК: задание 5, тема 4)
Обобщенной линейной множественной регрессией называется ЛРМ (ПТК: задание 1, тема 6)
Фиктивными переменными в уравнении множественной регрессии являются (ПТК: задание 3, тема 6)
Примером нелинейной зависимости экономических показателей является (ПТК: задание 2, тема 5)
В редакторе Excel построена регрессионная модель, имеются следующие данные (см. рисунок).
Модель содержит __1__ факторных признака и не содержит свободного слагаемого.
Параметр ___2___ (первый, второй) регрессионного уравнения является значимым, ___3__(первый, второй) параметр – не значим.
Все уравнение регрессии в целом ___4___(значимо, не значимо).
Коэффициент детерминации показывает, что __5__% вариации ____6___ (зависимой, независимой) переменной описывается построенным уравнением регрессии.
(ПТК: задание 5 темы 6)
Построена регрессионная модель вида (см. рисунок)
Интерпретируя коэффициенты уравнения можно указать
1) при ___1____(увеличении, уменьшении) фактора х1 на ___2__ результативный признак __3__ (возрастет, уменьшится) на ___4__, если второй фактор останется без изменения
2) при ___5____(увеличении, уменьшении) фактора х2 на ___6__ результативный признак __7__ (возрастет, уменьшится) на __8___, если первый фактор останется на неизменном уровне (ПТК: задание 4, тема 6)
После того как найдено уравнение регрессии, проводится оценка значимости, как уравнения в целом. Так и отдельных его параметров. Оценка значимости уравнения в целом дается с помощью критерия ___1____. При этом выдвигается нулевая гипотеза о ___2___ влияния фактора х на результат у. Если наблюдаемое значение критерия превышает табличное критическое значение, то уравнение регрессии в целом признается ___3___.
Оценка значимости коэффициентов регрессии проводится с помощью критерия ___4____. При этом выдвигается нулевая гипотеза и ___5____ параметра регрессии. Если расчетная статистика по абсолютной величине превышает табличное значение статистики, то параметр регрессии признается __6___. (ПТК: задание 3, тема 2)
(пропущенные слова вводить, соблюдая число, род и падеж по построению фразы).
Связь называется корреляционной, если каждому значению факторного признака соответствует (ПТК: задание 4, тема 3)
Коэффициент эластичности показывает (ПТК: задание 4, тема 5)
Предпосылками метода наименьших квадратов являются (ПТК: задание 1, тема 4)
Предопределенные переменные включают в себя (ПТК: задание 3, тема 2)
Идентификация модели – это (ПТК: задание 1, тема 10)
Системами эконометрических уравнений являются системы _______________ уравнений. (ПТК: задание 1, тема 12)
Линеаризация регрессий, нелинейных по переменным, но линейным по оцениваемым параметрам проводится методом (ПТК: задание 1-3, тема 5)
(более одного правильного ответа)
Синонимом системы взаимозависимых уравнений является система _____________ уравнений. (ПТК: задание 2, тема 9)
Лаговые значения переменных непосредственно включены в модель (ПТК: задание 3, тема 7)
(более одного правильного ответа)
При гетероскедастичности остатков регрессии применяют ______ метод наименьших квадратов. (ПТК: задание 1, тема 4)
Укажите методы уменьшения (устранения) автокорреляции во временных рядах (ПТК: задание 2, тема 7)
(более одного правильного ответа)
Соотнесите модели и понятия: (ПТК: задание 1, тема 7,8)
Если парный коэффициент корреляции между признаками Y и Х равен -1, то это означает (ПТК: задание 4, тема 2)
Обобщенный метод наименьших квадратов может применяться в случае нарушения предпосылок МНК о (ПТК: задание 3, тема 4)
Отбор факторов в модель множественной регрессии с использованием метода включения может быть основан на сравнении (ПТК: задание 3, тема 6)
При изучении трехфакторной регрессионной модели определитель матрицы парных коэффициентов корреляции имеет вид (см. рисунок)
(ПТК: задание 4, тема 6)
Система одновременных уравнений отличается от других видов эконометрических систем тем, что в ней (ПТК: задание 1, тема 12)
Принципиальные сложности применения системы эконометрических уравнений связаны с ошибками (ПТК: задание 2, тема 9)
Модель неидентифицируема, если число (ПТК: задание 1, тема 11)
Аддитивно мультипликативная модель содержит компоненты в виде _____ (отношений, слагаемых, сомножителей) (ПТК: задание 2, тема 9)
Структурной формой модели называется система _____ (независимых, взаимосвязанных, рекурсивных) уравнений. (ПТК: задание 1-3, тема 9)
Число степеней свободы связано с (ПТК: задание 3, тема 5)
Парный коэффициент корреляции не может принимать значение (ПТК: задание 4, тема 12)
В редакторе Excel построена регрессионная модель, имеются следующие данные (см. рисунок)
Модель содержит __1__ (два, три, четыре) факторных признака и не содержит свободного слагаемого. Параметр ___2___ (первый, второй) регрессионного уравнения является значимым, __3___(первый, второй) параметр – не значим. Все уравнение регрессии в целом ___4___(значимо, не значимо). Коэффициент детерминации показывает, что __5__% вариации ___6____ (зависимой, независимой) переменной описывается построенным уравнением регрессии. (ПТК: задания 3,4 тема 6)
Переменные, определяемые из уравнений модели, называются (ПТК: задание 4, тема 1)
Какие предположение из ниже представленных, не являются предпосылкой классической модели (ПТК: задание 3, тема 3)
Идентификация модели – это (ПТК: задание 1, тема 10)
Если парный коэффициент корреляции между признаками Y и Х принимает значение 0,675, то коэффициент детерминации равен (ПТК: задание 4, тема 2)
Свойства оценок параметров, полученных при помощи метода наименьших квадратов, предполагают исследование (ПТК: задание 2, тема 4)
С увеличением объема выборки (ПТК: задание 4, тема 5)
(более одного правильного ответа)
Оценивание случайной компоненты временного ряда проводится после (ПТК: задание 4, тема 8)
Мультиколлинеарность означает, что в модели регрессии матрица парных коэффициентов корреляции (ПТК: задание 4, тема 4)
Коэффициент детерминации может принимать значение (ПТК: задание 5, тема 4)
Диаграмма рассеяния указывает на нелинейную зависимость. В этом случае следует осуществлять (ПТК: задание 3, тема 5)
Если по одной и той же выборке рассчитаны регрессии Y на X и X на Y, то совпадут ли в этом случае линии регрессии? (ПТК: задание 5, тема 2)
Мы, ни раз, сдавали тесты по данному предмету и уверенно можем сказать: "Сделаем тест на хороший балл". Результаты сдачи, данного предмета, можете посмотреть во вкладке "Результаты"
Если необходима помощь, доверьте выполнения теста нам, так как, мы знакомы с Вашей системой тестирования.
Напишите нам, по любому каналу связи, размещённому на данной странице, мы проконсультируем Вас по условиям выполнения. При Вашем согласии, сделаем всё, чтобы Вам поставили хорошую оценку, по данному предмету.
Контакты
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
Написать нам в WhatsApp, Вы можете как с компьютера, через WhatsApp web, так и с мобильного приложения WhatsApp.
1. Для того чтобы написать с мобильного приложения, запишите в контакты наш номер телефона +7 962 146 0032 и пишите нам через мобильное приложение WhatsApp, как пишите своим знакомым.
2. Для удобства общения, можете написать нам с компьютера, нажмите на ССЫЛКУ
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1
- Откроется окно, в котором есть кнопка "НАПИСАТЬ" (рис. 1), нажимаете на неё:
Рис. 1

- Откроется окно WhatsApp web (это компьютерная версия приложения WhatsApp), если Вы ранее пользовалась WhatsApp web, Вы сразу перейдете в чат со мной, пишите сообщение и отправляйте (рис. 2).
Рис. 2
- Если Вы ни когда не использовали её, то Вы увидите окно с QR кодом и инструкцией как авторизоваться (пример данного окна изображен на рис.3)
Рис 3
- После сканирования мобильным приложением WhatsApp QR кода с экрана, Вы войдете в web версию WhatsApp. В окне Вы увидите все свои чаты, и будет активный чат с нами (рис. 2), пишите сообщение и отправляйте
Рис. 2
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
Viber: для поддержки наших заказчиков мы используем публичный аккаунт Vibera
1. Если у Вас Viber установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.
2. Если у Вас Viber в мобильном телефоне:
-
- Запустите мобильное приложение.
- Войдите в меню (три линии в нижнем правом углу экрана и надпись Ещё)

- Нажмите на иконку в правом верхнем углу - QR-код:

- Откроется квадратное окошко сканера, наведите его на изображение ниже этого сообщения, так чтобы оно все поместилось в окошко сканера:

- Откроется окно паблик аккаунта, нажимаете кнопку "Сообщение" и пишите нам:

- В дальнейшем, мы останемся у Вас в чатах, просто переходите в чат и пишите, как обычно пишите знакомым и друзьям.
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.

2. Если у Вас Telegram в мобильном телефоне:
- Запустите мобильное приложение Telegram и откройте поиск (в правом верхнем углу)

- В строке поиска вводите idkhelp_bot, когда будите вводить, внизу увидите наш чат бот, выглядит как на картинке внизу:

- Нажмите на него и далее внизу нажмите СТАРТ и пишите нам сообщение:

В дальнейшем, входите в историю сообщений и пишите нам.
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта:


